跳到主要内容

深度优先搜索（dfs）算法之三——寻路

3.1 例题一、迷宫​

题目描述​

给定一个 N×MN \times M 方格的迷宫，迷宫里有 TT 处障碍，障碍处不可通过。

在迷宫中移动有上下左右四种方式，每次只能移动一个方格。数据保证起点上没有障碍。

给定起点坐标和终点坐标，每个方格最多经过一次，问有多少种从起点坐标到终点坐标的方案。

输入格式​

第一行为三个正整数 N,M,TN,M,T，分别表示迷宫的长宽和障碍总数。

第二行为四个正整数 SX,SY,FX,FYSX,SY,FX,FY，SX,SYSX,SY 代表起点坐标，FX,FYFX,FY 代表终点坐标。

接下来 TT 行，每行两个正整数，表示障碍点的坐标。

输出格式​

输出从起点坐标到终点坐标的方案总数。

样例 #1​

样例输入 #1​
2 2 1
1 1 2 2
1 2
样例输出 #1​
1

提示​

对于 100%100\% 的数据，1≤N,M≤51 \le N,M \le 5，1≤T≤101 \le T \le 10，1≤SX,FX≤n1 \le SX,FX \le n，1≤SY,FY≤m1 \le SY,FY \le m。

迷宫
《迷宫 P1605》参考代码
#include <bits/stdc++.h>
using namespace std;
bool board[15][15];
int n,m,dx[4]={-1,+1,0,0},
        dy[4]={0,0,-1,+1};//定义四个方向的相对偏移，简化代码（行数）
int nx,ny,ex,ey,cnt;
//nx,ny起点坐标;ex,ey终点坐标,cnt路径条数
void dfs(int x,int y)
{
	if (x ==ex&&y ==ey)//如果到终点
	{
		cnt++;//路径加一
		return;//结束该线路向下递归
	} 
	for (int k=0;k<4;k++)
	{
		int l=x+dx[k];int r=y+dy[k];
		if (l>=1&&r>=1&&l<=n&&r<=m&&!board[l][r]) 
		{
			board[l][r]=1;//标记为已访问
			dfs(l,r);
			board[l][r]=0;//回溯
		}
	}
	return; 
}
int main ()
{
	int t,zx,zy;
	cin>>n>>m>>t>>nx>>ny>>ex>>ey;
	board[nx][ny]=1;
	while(t--)
	{
		cin>>zx>>zy;
		board[zx][zy]=2;//设为障碍
	} 
	dfs (nx,ny);//从起点开始寻找 
	cout<<cnt;
	return 0; 
}

3.2 例题二、下象棋​

题目描述​

在象棋盘(9*9)中，有一个马在坐标x行y列，现在想跳到n行m列，问在max步内，马有多少种跳到目标位置的方案（不考虑别马腿）？如果有，请输出所有的可能线路。

深搜将军抽车图例

输入格式​

一行 5 个整数，分别表示 x,y,n,m,max，出题人保证不越界 第二行 一个整数，棋盘上棋子个数num
后面num行，每行两个整数，分别是棋子的行和列

输出格式​

第一行输出一个整数，表示方案数
接下来若干行，每行一串坐标，从(x,y)到(n,m)一系列坐标，格式如：(3,3) (3,5) (4,6)，具体看样例。
最后一行一个整数，方案总数

输入/输出例子1​

输入：​
5 3 3 6 3
2
1 5
2 8

输出：​

(5 3) (3 4) (5 5) (3 6)
(5 3) (3 2) (4 4) (3 6)
(5 3) (3 2) (2 4) (3 6)
(5 3) (6 5) (4 4) (3 6)
(5 3) (6 5) (5 7) (3 6)
(5 3) (7 4) (5 5) (3 6)
(5 3) (4 5) (2 4) (3 6)
(5 3) (4 5) (5 7) (3 6)
8
参考代码
#include <bits/stdc++.h>
using namespace std;
char board[15][15]; //定义一个
int dx[] = {-2, -2, -1,  1,  1,  2, -1,  2}, 
        dy[] = { 1, -1, -2,  2, -2,  1,  2, -1}; //定义 8 个方向的相对偏移，简化代码（行数）

//cnt路径条数
int x,y,m,n,step,cnt,maxStep;
struct Txy {
    int r,c;
} ans[20];

void out( int step) {
    for (int i=0; i<=step; i++){
        cout <<"("<<ans[i].r<<" ";
        cout << ans[i].c<<") ";
    }
    cout << endl;
}

//x,y起点坐标;
void dfs(int x,int y,int step ) {
    ans[step].r=x;
    ans[step].c=y;
    if(step>maxStep) return;
    if(x==n && y==m) {
		cnt++;//找到一种方案，路径加一
        out(step);
		return;//结束该路线向下搜索
	} 
	for (int k=0;k<8;k++) {
        //r,c下一个预移动的目标地点的坐标
		int r=x+dx[k];int c=y+dy[k];
		if (r>=1 && c>=1 && r<=9 && c<=9 && !board[r][c]) 
		{
			board[r][c]=1;//标记为已访问
			dfs(r,c,step+1);
			board[r][c]=0;//回溯
		}
	}
}

int main () {
	cin>>x>>y>>n>>m>>maxStep;
	int t;
	cin>>t;
	while(t--){
		int r,c;
		cin>>r>>c;
		board[r][c]=2;
	}
	dfs (x,y,0);//从起点开始寻找 

	cout<<cnt;
	return 0; 
}

3.3 例题三、将军抽车​

根据《[语言月赛 202308] 小粉兔喜欢下象棋吗》 修改

题目描述​

在中国象棋中，马走日字形。用 (i,j)(i,j) 表示第 ii 行第 jj 列的格点，不考虑别马腿，考虑跳出棋盘外，在 (i,j)(i,j) 的马可以跳到 (i−2,j+1)(i-2,j+1)，(i−2,j−1)(i-2,j-1)，(i−1,j+2)(i-1,j+2)，(i−1,j−2)(i-1,j-2)，(i+1,j+2)(i+1,j+2)，(i+1,j−2)(i+1,j-2)，(i+2,j+1)(i+2,j+1)，(i+2,j−1)(i+2,j-1) 八个位置。

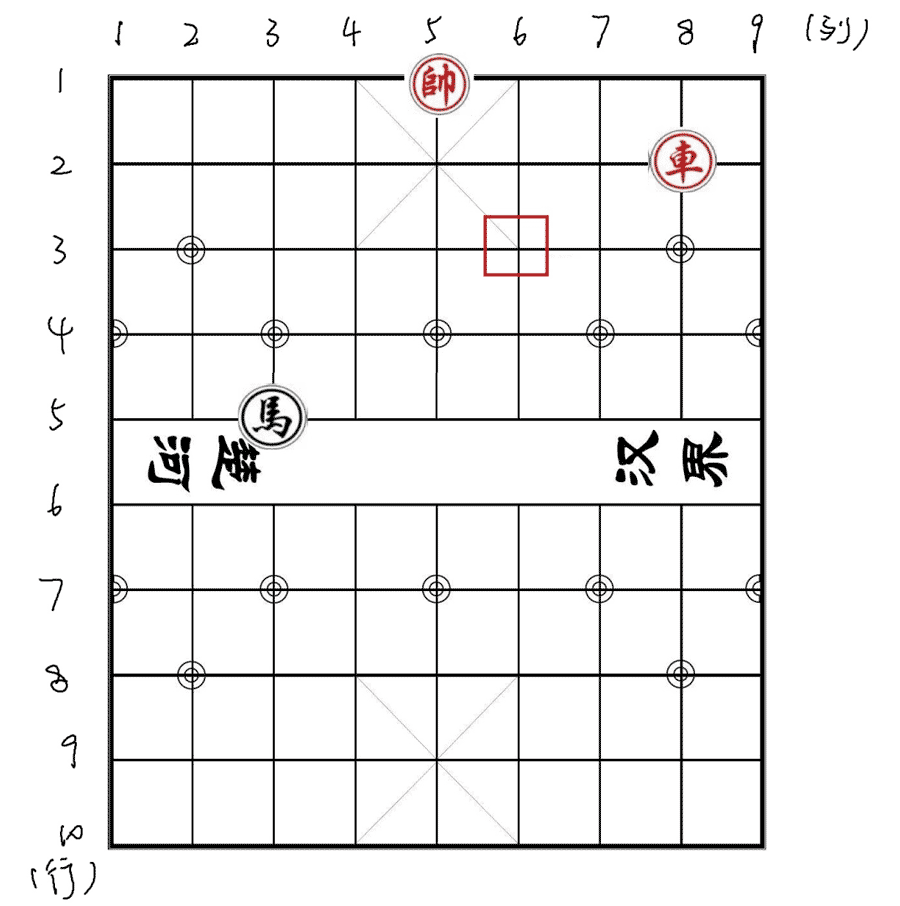
将军抽车是中国象棋中常用的进攻策略。如下图所示，此时红帅在 (1,5)(1,5)，红车在 (2,8)(2,8)。若黑马跳到红框位置所指的 (3,6)(3,6)，帅将由于被将军被迫移动，此时，马就可以吃掉红车。

深搜将军抽车图例

本题将解决将军抽车的简化版问题。在本题中，将军抽车就是要通过一步跳马，在能够将军的同时将车置于马的攻击位置。

只考虑棋盘上有红帅、红车、黑马各一枚的情况，不考虑帅是否可以通过移动实现对车的保护，不考虑别马腿。 你现在写一个程序帮助你思考下，在红车和红帅不移动的情况下，3步内，黑马是否可以在不出界的情况下，实现将军抽车？如果有，将每一步的坐标

输入格式​

输入共三行。 输入的第一行为两个整数 Sx,SyS_x,S_y，表示红帅的位置为 (Sx,Sy)(S_x,S_y)。
输入的第二行为两个整数 Cx,CyC_x,C_y，表示红车的位置为 (Cx,Cy)(C_x,C_y)。
输入的第三行为两个整数 Mx,MyM_x,M_y，表示黑马的位置为 (Mx,My)(M_x,M_y)。
保证红帅在 1∼31 \sim 3 行的九宫格内。

输出格式​

输出一行一个字符串：

  • 若可以实现将军抽车，输出 Yes。
  • 若不可以实现将军抽车，输出 No。

样例 #1​

样例输入 #1​
1 5
2 8
5 5
样例输出 #1​
Yes

样例 #2​

样例输入 #2​
1 5
2 9
5 5
样例输出 #2​
No

提示：​

数据规模与约定​

对于 100%100\% 的测试数据，1≤Sx≤31 \le S_x \le 3，4≤Sy≤64 \le S_y \le 6，1≤Cx,Mx≤101 \le C_x,M_x \le 10，1≤Cy,My≤91 \le C_y,M_y \le 9。保证没有任意两枚棋子初始时处于同一位置。

解题思路：​

  • 与上面的例题相似，其实就是求从一个点(n,m),从该点既可以跳到红帅也可以跳到红车的坐标
  • 同样是向八个方向进行深搜，不同的是结束条件（本题的目标点坐标需要求）
  • 结束条件怎么写呢？ 是不是检查八个方向是不是可以到达红帅和红车的坐标就可以了？ * 本题就留给大家自己去实现: 将军抽车
将军抽车示范代码

//检测是否可以同时到达红帅和红车
void check(int x,int y) {
    //此处就看你发挥了！~_~
    //todo:

    return false;
}

//x,y起点坐标;
void dfs(int x,int y,int step ) {
    ans[step].r=x;
    ans[step].c=y;
    if(step>maxStep) return;
    if(cnt && check(x,y)) {
		cnt++;//找到一种方案，路径加一
		return;//结束该路线向下搜索
	} 
	for (int k=0;k<8;k++) {
        //r,c下一个预移动的目标地点的坐标
        //...
	}
}

3.4 例题四、N 皇后​

一个如下的 6×66 \times 6 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行, 每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

n皇后示例图

上面的布局可以用序列 2 4 6 1 3 52\ 4\ 6\ 1\ 3\ 5 来描述，第 ii 个数字表示在第 ii 行的相应位置有一个棋子，如下：
行号 1 2 3 4 5 61\ 2\ 3\ 4\ 5\ 6
列号 2 4 6 1 3 52\ 4\ 6\ 1\ 3\ 5

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 33 个解。最后一行是解的总个数。

输入数据格式​

一行一个正整数 nn，表示棋盘是 n×nn \times n 大小的。

输出数据格式​

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

输入输出样例​

输入 #1输出 #1
6
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

说明与提示​

【数据范围】
对于 100%100\% 的数据，6≤n≤136 \le n \le 13。

题目翻译来自NOCOW。

USACO Training Section 1.5

解题思路：​

1、从上往下，先确定第一行放在哪 2、每一个行（递归层级）都有n种选择（有n列）可能 3、每种选择时需要判断水平、垂直、斜角是否有棋子放过 4、每一行为一层，向下递归

N皇后
#include<bits/stdc++.h>
using namespace std;
int n, queens[20];

int ans=0;

bool conflict(int row, int col) {
    for (int i = 1; i <= row; i++) {
        if (queens[i] == col || abs(queens[i] - col) == abs(i - row)) {
            return true;
        }
    }
    return false;
}
//将方案记录，或打印出来 
void print(){
    if(ans>3) return ;
    for (int i = 1; i <= n; i++) {

        cout<<queens[i]<<" ";        
    }
    cout<<endl;
}

void dfs(int x) {	   	      
    if (x==n+1){
        ans++;
        print();
        return ;
    } 
    for (int i=1; i<=n; i++)	{ //在该行选第几列 
        if (!conflict(x,i)) { //没有冲突该行该列就可以下棋
            queens[x] = i;
            dfs(x+1);
            queens[x] = -1; // 回溯
        }
    }
}

int main(){
    cin >> n ;		
    dfs(1);
    cout << ans;
    return 0;
}

扩展练习：​

  1. 将军抽车
  2. P1123 取数游戏

*学习笔记​

暂没有学习笔记，快来抢first blood ！