动态规划之一——基础
1.0 引言
1.1 动态规划(DP)定义
动态规划(Dynamic Programming,一般简称DP),是一种分阶段求解决策问题的数学思想。
那么如何更简单的理解动态规划的核心思想呢?
在国外版知乎有一个高赞的问答:
1.2 爬楼梯的三种解法
问题:每次可以爬1或2阶,求到第 n 阶的方案数。
解题过程一:数数找规律
解法1:递归
#include <bits/stdc++.h>
using namespace std;
int getWays(int n) {
if (n <= 0) {
return 0;
}
if (1 == n) {
return 1;
}
if (2 == n) {
return 2;
}
return getWays(n - 1) + getWays(n - 2);
}
int main()
{
int ret = getWays(10);
cout<<ret;
return 0;
}
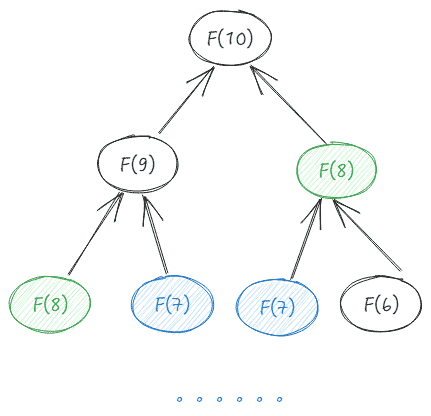
由上图可见,最终的结果是一个二叉树,二叉树的高度是n,
子节点的个数就是计算的次数为2^(n-1),所以最终的复杂度是O(2^n).
解法2:记忆化
由上图我们还可发现 F(8)、F(7)等重复递归多次,且值是一样的,于是可以用记忆化优化性能。
// twosum.cpp : 定义控制台应用程序的入口点。
//
#include <bits/stdc++.h>
using namespace std;
std::map<int, int> wayMap;
int getWays(int n) {
if (n <= 0) {
return 0;
}
if (1 == n) {
return 1;
}
if (2 == n) {
return 2;
}
if (wayMap.find(n) != wayMap.end()) {
return wayMap[n];
}
else {
int val = getWays(n - 1) + getWays(n - 2);
wayMap[n] = val;
return val;
}
}
int main()
{
int ret = getWays(10);
cout<<ret;
return 0;
}
时间复杂度和空间复杂度都是O(n).
解题过程二:倒着推
首先思考,假设n=10,如果只剩下最后一步就走到10级台阶,有几种情况。
只有两种: 一种是走到第8级,跳2级台阶走到10级;一种是走到第9级台阶,跳1级台阶走到10级。如果已知从第0级走到第8级的走法有X种,从第0级走到第9级的走法有Y种,那么从第0级走到第10级的走法就有X+Y种。
写成公式,可以表达为F(10) = F(9) + F(8);
依次类推,F(9) = F(8)+F(7); F(8) = F(7)+F(6);
最后归纳为:
当只有1级台阶和2级台阶的时候,走法只有1种和2种。也就是说
F(1) = 1; F(2) = 2; F(n) = F(n)+F(n-1);
也就是第n步只依赖前面的 n-1 和 n-2 的方案数,那么我们只要先求出第1阶和第2阶的方案数(固定的)就可以求出第3阶,再就可以求出第4阶,以此类推,于是得到了动态规划的解法:
解法3:动态规划
#include <bits/stdc++.h>
#defined N=100+5;
using namespace std;
int dp[N];
int getWays(int n) {
f[1]=1;
f[2]=2;
for (int i = 3; i <= n; i++) {
f[i]=f[i-1]+f[i-2];
}
return f[n];
}
int main()
{
int ret = getWays(10);
cout<<ret;
return 0;
}
1.3 小结
用动态规划来解决问题,就是将复杂问题分解为相互关联的 子问题,并用一个或多个变量(通常记为 dp[...])表示子问题的解。 例如:在以上爬楼梯的问题中,我们将一个N台阶方案数的问题转化为求子问题(更小的规模的问题)(N-1和N-2)。
其中涉及到动态规划的几个重要概念:
最优子结构:
也就是与子问题的关系,该题中就是 F(n) = F(n-1)+F(n-2)
状态:
dp[i]表示到第i级台阶的方案数(解)
边界:
边界是 F(1)和F(0),它们两个的值是确定的,可以理解为特殊情况,等同于递归函数的边界条件。
状态转换方程:
状态转移公式是dp[i] = dp[i-1]+dp[i-2]
1.4 走楼梯2
有N台阶的楼梯,��每个台阶上有个数字。你从第1台阶开始,每次可以有3种向上的走法:上1个台阶、上2个台阶、上3个台阶。要求刚好到达最高的第N个台阶,问怎样走,走到的台阶上的数字和最小?
例如下面是一个6个台阶的示意图:
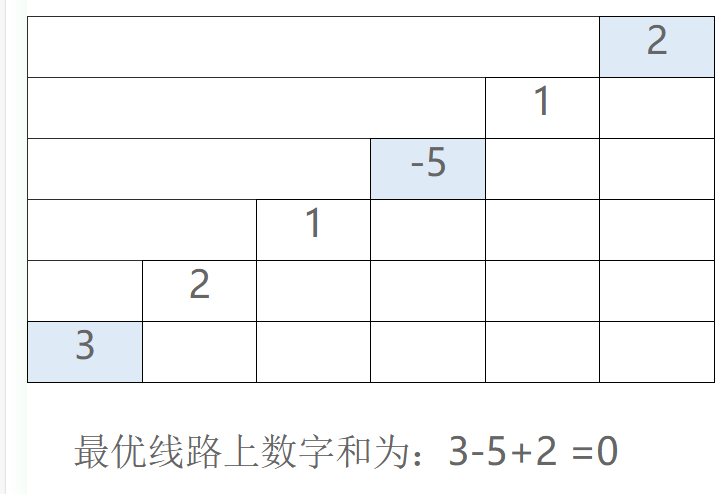
输入格式
第1行:1个正整数N,范围[2,100]。
第2行N个整数,每个整数范围[-100,100]
输出格式
一个整数。
输入/输出例子1
输入:
8
1 2 3 4 5 6 -3 0
输出:
2
状态定义:
dp[i] 表示到第i个台阶的最小和
状态转移方程:
dp[i] = min(dp[i-1],dp[i-2],dp[i-3])+A[i]
边界:
- 为了简化程序,dp[0]也算上,但是它不能走,可以初始化为一个极大值;
- dp[1]=A[1],dp[2]=A[1]+A[2]
#include <bits/stdc++.h>
using namespace std;
int n;
int f[105],dp[105];
int main()
{
cin >> n ;
for (int i=1; i<=n; i++)
cin >> f[i];
dp[0]=0x7f7f7f7f;
dp[1]=f[1];
dp[2]=f[2]+f[1];
int m;
for (int i=3; i<=n; i++){
m = min(dp[i-1],dp[i-2]);
dp[i] = min(m,dp[i-3])+f[i];
}
cout << dp[n] <<endl;
return 0;
}
1.5 “动态规划”名词释义
动态规划(Dynamic Programming)这一名称的由来可以追溯到其创始人**理查德·贝尔曼(Richard Bellman)**在20世纪50年代的研究背景和命名意图。以下是详细解释:
名称的构成:动态(Dynamic)与规划(Programming)
-
动态(Dynamic)
表示问题具有多阶段决策特性,每个阶段的决策会影响后续状态的变化。例如:- 在最短路径问题中,每一步的选择会影响后续路径的选项。
- 在背包问题中,是否选择当前物品会影响剩余容量和后续选择。
- 这种“随时间或阶段推进而变化”的特性,体现了“动态”的本质。
-
规划(Programming)
这里的“规划”并非指计算机编程,而是数学中的术语,意�为系统化的优化过程。例如:- 线性规划(Linear Programming)是通过线性模型寻找最优解。
- 动态规划则是通过定义状态和状态转移方程,系统地求解多阶段优化问题。
命名背景
贝尔曼在兰德公司研究军事和工程中的多阶段决策问题时,提出了这一方法。他在自传中提到:
- “动态”:强调问题在不同阶段的动态变化和依赖关系。
- “规划”:借鉴数学优化领域的术语(如线性规划),表示通过系统化的步骤寻找最优解。
- 幽默的考量:贝尔曼曾调侃,选择“动态”一词是因为当时美国国防部对“动态”一词有偏好,更容易获得资助。
与其他方法的区别
- 分治法(Divide and Conquer):
将问题分解为独立的子问题,递归解决后合并结果(如归并排序)。子问题之间无重叠。 - 动态规划:
子问题存在重叠,通过记忆化(Memoization)或表格存储避免重复计算,体现“动态”调整和状态转移。
动态规划的核心思想
- 状态定义:用变量(如
dp[i][j])描述问题的子结构。 - 状态转移方程:建立子问题间的递推关系(如
dp[i] = dp[i-1] + dp[i-2])。 - 记忆化存储:保存已计算的子问题结果,避免重复计算。
总结
动态规划的名称体现了其核心特点:
- 动态:处理多阶段、状态依赖的优化问题。
- 规划:通过系统化的状态定义和转移方程实现高效求解。
贝尔曼的命名既反映了方法的数学本质,也带有时代背景的趣味性。这一方法通过“记住过去,优化未来”,成为解决复杂问题的利器。
1.6 核心:状态定义
状态定义:将复杂问题分解为相互关联的 子问题,并用一个或多个变量(通常记为 dp[...])表示子问题的解。
状态的意义:每个状态需要 完整描述 当前子问题的特征(类似记忆化搜索的参数/维度),以便推导后续状态。
无后效性(Non-Aftereffect Property):
动态规划的核心特征之一是 无后效性,即:
“未来的决策仅依赖于当前状态,而不依赖于过去如何到达当前状态的路径。”
这意味着:
- 如果两个不同的路径到达同一个状态,它们对后续决策的影响必须完全相同。
- 如果状态定义缺失关键信息,导致后续决策需要依赖历史路径,则状态设计失败。
用动态规划来解决问题的核心就是状态定义:
-
决定问题的可解性
-
正确的状态定义是推导状态转移方程的前提。
-
错误的状态定义可能导致无法覆盖所有情况或状态爆炸。
-
-
影响时间与空间复杂度
-
状态维度过高 → 时间复杂度指数级增长。
-
状态定义冗余 → 空间复杂度浪费。
-
-
反映问题本质
- 状态必须包含足够的信息,确保后续决策独立于历史路径(满足 无后效性)。
思考:
之前用dfs做的题,哪些可以用DP做? 如果不可以,为什么?




