动态规划之二——线性DP入门

2.1 P1115 最大子段和

题目描述

给出一个长度为 $n$ 的序列 $a$ ，选出其中连续且非空的一段使得这段和最大。

输入格式

第一行是一个整数，表示序列的长度 $n$ 。

第二行有 $n$ 个整数，第 $i$ 个整数表示序列的第 $i$ 个数字 $a_i$ 。

输出格式

输出一行一个整数表示答案。

输入输出样例 #1

输入 #1

7
2 -4 3 -1 2 -4 3

输出 #1

说明/提示

######## 样例 1 解释

选取 $[3, 5]$ 子段 $\{3, -1, 2\}$ ，其和为 $4$ 。

######## 数据规模与约定

对于 $40\%$ 的数据，保证 $n \leq 2 \times 10^3$ 。
对于 $100\%$ 的数据，保证 $1 \leq n \leq 2 \times 10^5$ ， $-10^4 \leq a_i \leq 10^4$ 。

初始思路

最直接的想法是，枚举所有可能的连续子数组，并计算它们的和，然后找出最大的那个。

#include <bits/stdc++.h>
using namespace std;

int main() {
  int n;
  cin >> n;
  int a[n];
  for(int i=0; i<n; i++) cin >> a[i];
  
  int max_sum = INT_MIN;
  for(int i=0; i<n; i++) {
      int current_sum = 0;
      for(int j=i; j<n; j++) {
          current_sum += a[j];
          if(current_sum > max_sum) {
              max_sum = current_sum;
          }
      }
  }
  cout << max_sum << endl;
  return 0;
}

但这个的时间复杂度是 O(n^2),我们需要考虑更高效的做法,比如动态规划.

动态规划解决

状态定义:

我们定义dp[i]表示以第i个元素结尾的最大连续子序列和，然后通过遍历序列，不断更新这个数组的值。这样，最终结果就是这个数组中的最大值
dp[i] 与前面的dp[i-1]是什么关系 ?
- 1~i 的和是不是等于 dp[i-1] + nums[i]?
- 有什么特殊问题需要考虑? 负数
- 如果前一个元素的最大连续子序列和是负数，那么当前元素的最优解就是其本身；如果前一个是正数，则当前元素加上前一个的最大值才是最优解。

状态转移方程:
dp[i] = max(a[i], dp[i-1] + a[i])

#include <bits/stdc++.h> // 用于max函数
const int N=2e5;
using namespace std;
int dp[N];

int main() {
  int n;
  cin >> n;
  int a[n];
  for(int i=0; i<n; i++) cin >> a[i];

  dp[0] = a[0];
  int max_sum = dp[0];
  
  for(int i=1; i<n; i++) {
      dp[i] = max(a[i], dp[i-1] + a[i]);
      max_sum = max(max_sum, dp[i]);
  }
  
  cout << max_sum << endl;
  return 0;
}

初始思路

最直接的想法是，枚举所有可能的连续子数组，并计算它们的和，然后找出最大的那个。

#include <bits/stdc++.h>
using namespace std;

int main() {
  int n;
  cin >> n;
  int a[n];
  for(int i=0; i<n; i++) cin >> a[i];
  
  int max_sum = INT_MIN;
  for(int i=0; i<n; i++) {
      int current_sum = 0;
      for(int j=i; j<n; j++) {
          current_sum += a[j];
          if(current_sum > max_sum) {
              max_sum = current_sum;
          }
      }
  }
  cout << max_sum << endl;
  return 0;
}

但这个的时间复杂度是 O(n^2),我们需要考虑更高效的做法,比如动态规划.

动态规划解决

状态定义:

我们定义dp[i]表示以第i个元素结尾的最大连续子序列和，然后通过遍历序列，不断更新这个数组的值。这样，最终结果就是这个数组中的最大值
dp[i] 与前面的dp[i-1]是什么关系 ?
- 1~i 的和是不是等于 dp[i-1] + nums[i]?
- 有什么特殊问题需要考虑? 负数
- 如果前一个元素的最大连续子序列和是负数，那么当前元素的最优解就是其本身；如果前一个是正数，则当前元素加上前一个的最大值才是最优解。

状态转移方程:
dp[i] = max(a[i], dp[i-1] + a[i])

#include <bits/stdc++.h> // 用于max函数
const int N=2e5;
using namespace std;
int dp[N];

int main() {
  int n;
  cin >> n;
  int a[n];
  for(int i=0; i<n; i++) cin >> a[i];

  dp[0] = a[0];
  int max_sum = dp[0];
  
  for(int i=1; i<n; i++) {
      dp[i] = max(a[i], dp[i-1] + a[i]);
      max_sum = max(max_sum, dp[i]);
  }
  
  cout << max_sum << endl;
  return 0;
}

2.2 P1216 [IOI 1994] 数字三角形 Number Triangles

题目描述

观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

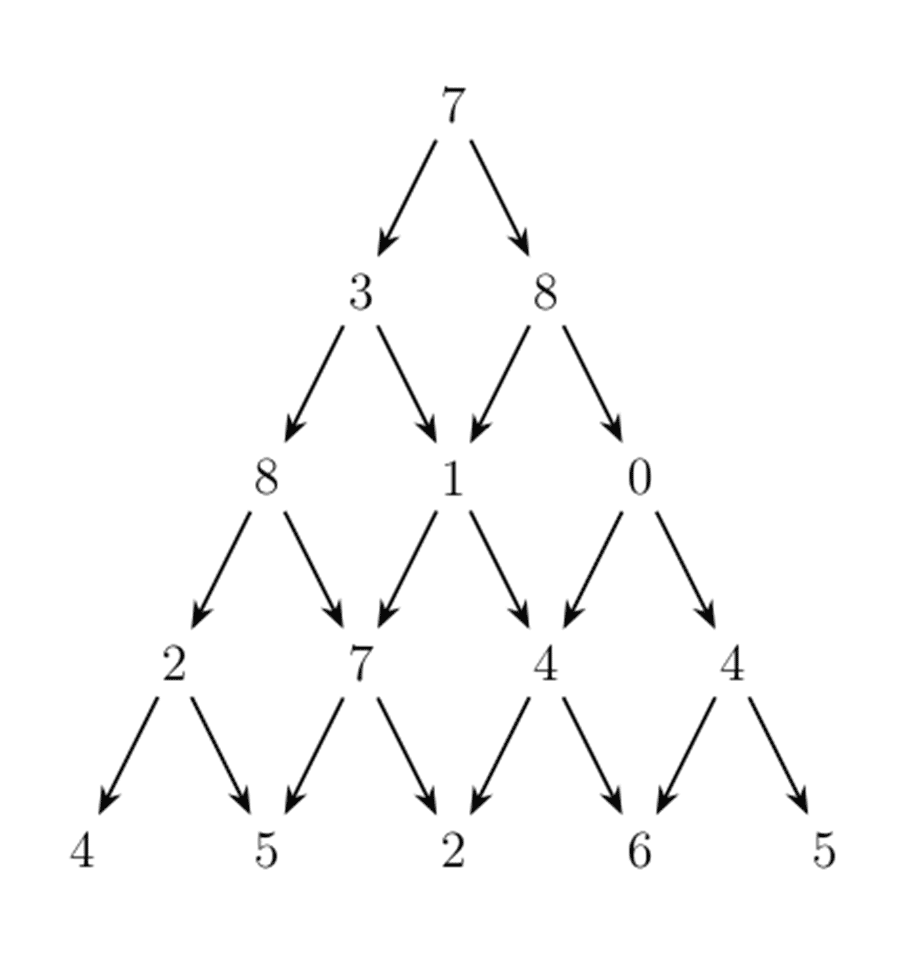
数字三角形

在上面的样例中，从 $7 \to 3 \to 8 \to 7 \to 5$ 的路径产生了最大权值。

输入格式

第一个行一个正整数 $r$ ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式

单独的一行,包含那个可能得到的最大的和。

输入输出样例 #1

输入 #1

输出 #1

说明/提示

【数据范围】
对于 $100\%$ 的数据， $1\le r \le 1000$ ，所有输入在 $[0,100]$ 范围内。

题目翻译来自NOCOW。

USACO Training Section 1.5

IOI1994 Day1T1

复杂度对比

方法	时间复杂度	空间复杂度	特点
自底向上	O(n²)	O(n²)	结果直接位于顶点
自顶向下	O(n²)	O(n²)	需遍历最后一层找最大值
滚动数组优化	O(n²)	O(n)	适用于大规模数据

题意初步分析：
给定数字三角形，从顶部到底部选择路径，每次只能向下或右下移动，求最大路径和。
示例输入（5层）：

最大路径：7→3→8→7→5，总和30

暴力枚举：

路径总数 = 2^(n-1) → 指数级复杂度
画出所有路径树，标出重复计算的子路径

关键提问：
"如何避免重复计算相同子路径？能否用记忆化方式存储中间结果？"

状态定义：

dp[i][j]：从顶部到位置(i,j)到最大路径和

转移方程推导：

对每个位置(i,j)，选择上方或左上方较大的路径

方程：

dp[i][j] = a[i][j] + max(dp[i-1][j], dp[i-1][j-1])

在最后一层中寻找最大值

示例dp表填充（简化版）：

原数据：        dp数组最终状态：
  7                  7
 3 8               10  15
8 1 0           18   16  15
2 7 4 4       20   25   20   19
4 5 2 6 5   24   30   27   26   24

#include <bits/stdc++.h>
using namespace std;
const int N=1005;
int a[N][N],dp[N][N];
int main() {
  int n;
  cin >> n;
  
  // 读取三角形数据（左下对齐）
  for(int i=1; i<=n; i++) {
      for(int j=1; j<=i; j++) {
          cin >> a[i][j];
          dp[i][j]=a[i][j];
      }
  }
  
  // 正向递推（自顶向下）
  for(int i=1; i<=n; i++) {         // 从第二层开始
      for(int j=1; j<=i; j++) {    // 每层有i+1个元素
          // 取上方两个位置的最大值
          dp[i][j] += max(dp[i-1][j-1], dp[i-1][j]);
      }
  }
  
  // 输出最后一层的最大值
  cout << *max_element(dp[n]+1, dp[n]+n+1) << endl;
  
  return 0;
}

是否可以倒推？

状态定义：

dp[i][j]：从位置(i,j)到底层的最大路径和
逆向思维：从底层开始计算，逐步向上汇总

转移方程推导：

对每个位置(i,j)，选择下方或右下方较大的路径

方程：

dp[i][j] = a[i][j] + max(dp[i+1][j], dp[i+1][j+1])

用示例数据逐层填写dp表（从底层向上）

示例dp表填充：

原数据：        dp数组最终状态：
  7              30
 3 8           23  21
8 1 0        20  13  10
2 7 4 4      7  12  10  10
4 5 2 6 5    4   5   2   6   5

#include <bits/stdc++.h>
using namespace std;
const int N=1005;
int a[N][N],dp[N][N];

int main() {
  int n;
  cin >> n;
  
  // 读取三角形数据（左下对齐）
  for(int i=0; i<n; i++) {
      for(int j=0; j<=i; j++) {
          cin >> a[i][j];
          dp[i][j]=a[i][j]; // 初始化dp数组为原始数据副本
      }
  }
  
  
  // 自底向上递推
  for(int i=n-2; i>=0; i--) {      // 从倒数第二层开始
      for(int j=0; j<=i; j++) {    // 每层有i+1个元素
          dp[i][j] += max(dp[i+1][j], dp[i+1][j+1]);
      }
  }
  
  cout << dp[0][0] << endl;
  return 0;
}

关键技巧：

输入数据按三角形左下对齐存储
i 从n-2开始逆推（最后一层无需计算）
时间复杂度O(n²)，空间复杂度O(n²)

空间优化（滚动数组法）

优化思路：

观察状态转移：每层计算只依赖下一层的数据
只需维护一维数组，覆盖旧数据

优化代码：

#include <bits/stdc++.h>
using namespace std;
int a[N][N],dp[N];

int main() {
  int n;
  cin >> n;
  
  for(int i=0; i<n; i++) {
      for(int j=0; j<=i; j++) {
          cin >> a[i][j];
      }
  }
  // 初始化dp为最后一层
  for(int i=0; i<n; i++) {
      dp[i]=a[n-1][i];
  }
  
  for(int i=n-2; i>=0; i--) {
      for(int j=0; j<=i; j++) {
          dp[j] = a[i][j] + max(dp[j], dp[j+1]);
      }
  }
  
  cout << dp[0] << endl;
  return 0;
}

复杂度对比

方法	时间复杂度	空间复杂度	特点
自底向上	O(n²)	O(n²)	结果直接位于顶点
自顶向下	O(n²)	O(n²)	需遍历最后一层找最大值
滚动数组优化	O(n²)	O(n)	适用于大规模数据

题意初步分析：
给定数字三角形，从顶部到底部选择路径，每次只能向下或右下移动，求最大路径和。
示例输入（5层）：

最大路径：7→3→8→7→5，总和30

暴力枚举：

路径总数 = 2^(n-1) → 指数级复杂度
画出所有路径树，标出重复计算的子路径

关键提问：
"如何避免重复计算相同子路径？能否用记忆化方式存储中间结果？"

状态定义：

dp[i][j]：从顶部到位置(i,j)到最大路径和

转移方程推导：

对每个位置(i,j)，选择上方或左上方较大的路径

方程：

dp[i][j] = a[i][j] + max(dp[i-1][j], dp[i-1][j-1])

在最后一层中寻找最大值

示例dp表填充（简化版）：

原数据：        dp数组最终状态：
  7                  7
 3 8               10  15
8 1 0           18   16  15
2 7 4 4       20   25   20   19
4 5 2 6 5   24   30   27   26   24

#include <bits/stdc++.h>
using namespace std;
const int N=1005;
int a[N][N],dp[N][N];
int main() {
  int n;
  cin >> n;
  
  // 读取三角形数据（左下对齐）
  for(int i=1; i<=n; i++) {
      for(int j=1; j<=i; j++) {
          cin >> a[i][j];
          dp[i][j]=a[i][j];
      }
  }
  
  // 正向递推（自顶向下）
  for(int i=1; i<=n; i++) {         // 从第二层开始
      for(int j=1; j<=i; j++) {    // 每层有i+1个元素
          // 取上方两个位置的最大值
          dp[i][j] += max(dp[i-1][j-1], dp[i-1][j]);
      }
  }
  
  // 输出最后一层的最大值
  cout << *max_element(dp[n]+1, dp[n]+n+1) << endl;
  
  return 0;
}

是否可以倒推？

状态定义：

dp[i][j]：从位置(i,j)到底层的最大路径和
逆向思维：从底层开始计算，逐步向上汇总

转移方程推导：

对每个位置(i,j)，选择下方或右下方较大的路径

方程：

dp[i][j] = a[i][j] + max(dp[i+1][j], dp[i+1][j+1])

用示例数据逐层填写dp表（从底层向上）

示例dp表填充：

原数据：        dp数组最终状态：
  7              30
 3 8           23  21
8 1 0        20  13  10
2 7 4 4      7  12  10  10
4 5 2 6 5    4   5   2   6   5

#include <bits/stdc++.h>
using namespace std;
const int N=1005;
int a[N][N],dp[N][N];

int main() {
  int n;
  cin >> n;
  
  // 读取三角形数据（左下对齐）
  for(int i=0; i<n; i++) {
      for(int j=0; j<=i; j++) {
          cin >> a[i][j];
          dp[i][j]=a[i][j]; // 初始化dp数组为原始数据副本
      }
  }
  
  
  // 自底向上递推
  for(int i=n-2; i>=0; i--) {      // 从倒数第二层开始
      for(int j=0; j<=i; j++) {    // 每层有i+1个元素
          dp[i][j] += max(dp[i+1][j], dp[i+1][j+1]);
      }
  }
  
  cout << dp[0][0] << endl;
  return 0;
}

关键技巧：

输入数据按三角形左下对齐存储
i 从n-2开始逆推（最后一层无需计算）
时间复杂度O(n²)，空间复杂度O(n²)

空间优化（滚动数组法）

优化思路：

观察状态转移：每层计算只依赖下一层的数据
只需维护一维数组，覆盖旧数据

优化代码：

#include <bits/stdc++.h>
using namespace std;
int a[N][N],dp[N];

int main() {
  int n;
  cin >> n;
  
  for(int i=0; i<n; i++) {
      for(int j=0; j<=i; j++) {
          cin >> a[i][j];
      }
  }
  // 初始化dp为最后一层
  for(int i=0; i<n; i++) {
      dp[i]=a[n-1][i];
  }
  
  for(int i=n-2; i>=0; i--) {
      for(int j=0; j<=i; j++) {
          dp[j] = a[i][j] + max(dp[j], dp[j+1]);
      }
  }
  
  cout << dp[0] << endl;
  return 0;
}

复杂度对比

方法	时间复杂度	空间复杂度	特点
自底向上	O(n²)	O(n²)	结果直接位于顶点
自顶向下	O(n²)	O(n²)	需遍历最后一层找最大值
滚动数组优化	O(n²)	O(n)	适用于大规模数据

2.3 B3637 最长上升子序列

题目描述

这是一个简单的动规板子题，简称LIS(Longest Increasing Subsequence)。

给出一个由 $n(n\le 5000)$ 个不超过 $10^6$ 的正整数组成的序列。请输出这个序列的最长上升子序列的长度。

最长上升子序列是指，从原序列中按顺序取出一些数字排在一起，这些数字是逐渐增大的。

输入格式

第一行，一个整数 $n$ ，表示序列长度。

第二行有 $n$ 个整数，表示这个序列。

输出格式

一个整数表示答案。

输入输出样例 #1

输入 #1

6
1 2 4 1 3 4

输出 #1

输入 #2

10
1 5 7 2 4 3 5 4 8 5

输出 #2

说明/提示

分别取出 $1$ 、 $2$ 、 $3$ 、 $4$ 即可。

#include <bits/stdc++.h>
using namespace std;

int main() {
  int n;
  cin >> n;
  vector<int> a(n);
  for(int i=0; i<n; i++) cin >> a[i];
  
  vector<int> dp(n, 1); // 初始化为1
  
  for(int i=1; i<n; i++) {
      for(int j=0; j<i; j++) {
          if(a[j] < a[i]) {
              dp[i] = max(dp[i], dp[j]+1);
          }
      }
  }
  
  cout << *max_element(dp.begin(), dp.end()) << endl;
  return 0;
}

状态定义：
dp[i] 表示以第 i 个元素结尾的最长上升子序列的长度。

举例分析: 序列：[3,1,4,1,5]
以第0个元素结尾:dp[0] = 1（只有3,所以长度是1）
以第1个元素结尾:dp[1] = 1（只有3或1,所以长度还是1）
以第2个元素结尾:dp[2] = dp[1]+ 1 → 2（1和4,最大长度为2）

是不是后续都可以这样推理?
有什么"特殊"情况或需要分类处理?

状态转移方程: 遍历 j 从 0 到 i-1

若 a[j] < a[i]，则 dp[i] = max(dp[i], dp[j]+1)

for(int j=0; j<i; j++) {
  if(a[j] < a[i]) {
      dp[i] = max(dp[i], dp[j] + 1);
  }
}

初始状态：
dp[i] = 1（每个元素本身可以作为一个长度为1的上升子序列）。

索引	0	1	2	3	4
a[i]	3	1	4	1	5
dp[i]	1	1	2	1	3

#include <bits/stdc++.h>
using namespace std;
const int N=5005;
int a[N],dp[N];
int main() {
  int n;
  cin >> n;
  // 读取输入并初始化dp
  for(int i=0; i<n; i++) {
      cin >> a[i];
      dp[i] = 1; // 初始化为1
  }
  
  // 动态规划计算LIS
  for(int i=1; i<n; i++) {
      for(int j=0; j<i; j++) {
          if(a[j] < a[i]) {
              dp[i] = max(dp[i], dp[j]+1);
          }
      }
  }
  // 输出最大值
  int maxdp=0;
  for(int i=0;i<n;i++)
      if(dp[i]>maxdp) maxdp=dp[i];
  cout<< maxdp<<endl;
  //cout << *max_element(dp, dp + n) << endl;
  
  return 0;
}

#include <bits/stdc++.h>
using namespace std;

int main() {
  int n;
  cin >> n;
  vector<int> a(n);
  for(int i=0; i<n; i++) cin >> a[i];
  
  vector<int> dp(n, 1); // 初始化为1
  
  for(int i=1; i<n; i++) {
      for(int j=0; j<i; j++) {
          if(a[j] < a[i]) {
              dp[i] = max(dp[i], dp[j]+1);
          }
      }
  }
  
  cout << *max_element(dp.begin(), dp.end()) << endl;
  return 0;
}

状态定义：
dp[i] 表示以第 i 个元素结尾的最长上升子序列的长度。

是不是后续都可以这样推理?
有什么"特殊"情况或需要分类处理?

状态转移方程: 遍历 j 从 0 到 i-1

若 a[j] < a[i]，则 dp[i] = max(dp[i], dp[j]+1)

for(int j=0; j<i; j++) {
  if(a[j] < a[i]) {
      dp[i] = max(dp[i], dp[j] + 1);
  }
}

初始状态：
dp[i] = 1（每个元素本身可以作为一个长度为1的上升子序列）。

索引	0	1	2	3	4
a[i]	3	1	4	1	5
dp[i]	1	1	2	1	3

#include <bits/stdc++.h>
using namespace std;
const int N=5005;
int a[N],dp[N];
int main() {
  int n;
  cin >> n;
  // 读取输入并初始化dp
  for(int i=0; i<n; i++) {
      cin >> a[i];
      dp[i] = 1; // 初始化为1
  }
  
  // 动态规划计算LIS
  for(int i=1; i<n; i++) {
      for(int j=0; j<i; j++) {
          if(a[j] < a[i]) {
              dp[i] = max(dp[i], dp[j]+1);
          }
      }
  }
  // 输出最大值
  int maxdp=0;
  for(int i=0;i<n;i++)
      if(dp[i]>maxdp) maxdp=dp[i];
  cout<< maxdp<<endl;
  //cout << *max_element(dp, dp + n) << endl;
  
  return 0;
}

#include <bits/stdc++.h>
using namespace std;

int main() {
  int n;
  cin >> n;
  vector<int> a(n);
  for(int i=0; i<n; i++) cin >> a[i];
  
  vector<int> dp(n, 1); // 初始化为1
  
  for(int i=1; i<n; i++) {
      for(int j=0; j<i; j++) {
          if(a[j] < a[i]) {
              dp[i] = max(dp[i], dp[j]+1);
          }
      }
  }
  
  cout << *max_element(dp.begin(), dp.end()) << endl;
  return 0;
}

扩展练习：

*学习笔记

暂没有学习笔记，快来抢first blood ！

2.1 P1115 最大子段和​

题目描述​

输入格式​

输出格式​

输入输出样例 #1​

输入 #1​

输出 #1​

说明/提示​

初始思路

2.2 P1216 [IOI 1994] 数字三角形 Number Triangles​

题目描述​

输入格式​

输出格式​

输入输出样例 #1​

输入 #1​

输出 #1​

说明/提示​

2.3 B3637 最长上升子序列​

题目描述​

输入格式​

输出格式​

输入输出样例 #1​

输入 #1​

输出 #1​

输入 #2​

输出 #2​

说明/提示​

扩展练习：​

*学习笔记​

2.1 P1115 最大子段和

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

说明/提示

2.2 P1216 [IOI 1994] 数字三角形 Number Triangles

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

说明/提示

2.3 B3637 最长上升子序列

题目描述

输入格式

输出格式

输入输出样例 #1

输入 #1

输出 #1

输入 #2

输出 #2

说明/提示

扩展练习：

*学习笔记