深度优先搜索(dfs)算法之二——枚举&排列
1.1 指数型枚举
从 1 ~ n 这 n 个整数中随机选取任意多个,输出所有可能的选择方案。
输入格式
输入一个整数 n。
输出格式
每行输出一种方案。 同一行内的数必须升序排列,相邻两个数用恰好 1 个空格隔开。 对于没有选任何数的方案,输出空行。 本题有自定义校验器(SPJ),各行(不同方案)之间的顺序任意。
数据范围
1 ≤ n ≤ 15
输入样例:
3
输出样例:
3
2
23
1
13
12
123
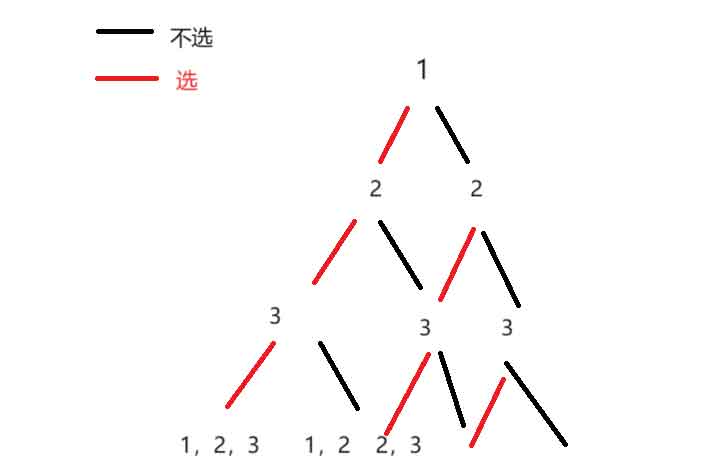
指数型枚举是指一共有n个数,每一个数都有两种状态,也就是选或不选,时间复杂度也就是2^n,指数级的 例如3个数的枚举时,每一个数都有选和不选两种状态,可以根据这个画出递归搜索树:
#include <iostream>
using namespace std;
int n;
int vis[20];
void dfs(int x){
//表示已经n个数都被判断过了,一种方案已经搜索完成
if(x > n){
for(int i = 1;i <= n;i++){
if(vis[i] == 1)
cout<<i<<" ";
}
cout<<'\n';
return;
}
vis[x] = 2;//表示不选
dfs(x+1);//继续搜下一个
vis[x] = 0;//回溯
vis[x] = 1;//表示选
dfs(x+1);//继续搜下一个
vis[x] = 0;//回溯
}
int main(){
cin>>n;
dfs(1);
return 0;
}
2.2 排列型枚举
排列型枚举是一种生成给定集合所有可能排列的方法,其实在中学阶段我们就学过排列组合的问题,排列是区分顺序的,例如,同样是1 2 3三个数字,1,2, 3和 1,3,2是两种方案。 来看下面的一个例题:
题目描述
按照字典序输出自然数 1 到 n 所有不重复的排列,即 n 的全排列,要求所产生的任一数字序列中不允许出现重复的数字。
输入格式
一个整数 n。
输出格式
由 1 ~ n 组成的所有不重复的数字序列,每行一个序列。
每个数字保留 5 个场宽。
输入输出样例
输入 #1
3
输出 #1
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
说明/提示
1 ≤ n ≤ 9。
解题思路就是生成n个数字的全排列方案,在用代码实现的过程中,需要另外再开一个vis数组,表示状态,以此来区分是否被选过。
#include <bits/stdc++.h>
using namespace std;
int vis[15];
int a[15];
int n;
void dfs(int x){
//表示n个数字都已经选过了
if(x > n){
for(int i = 1;i <= n;i++){
cout<<setw(5)<<a[i];//题目中要求5个场宽
}
cout<<'\n';
return;
}
for(int i = 1;i <= n;i++){
if(!vis[i]){
vis[i] = 1;//选过标记为1
a[x] = i;//表示该数字被选上了
dfs(x+1);//继续选下一个数字
vis[i] = 0;//回溯重置该数字的状态
a[x] = 0;//,也可以不写,因为数据可以直接覆盖
}
}
}
int main(){
cin>>n;
dfs(1);
return 0;
}
2.3 组合型枚举
组合是从n个不同元素中取出m(m≤n)个元素的所有取法,组合不考虑元素的顺序。也就是 1 2 3 和 1 3 2是同一种方案
题目描述
排列与组合是常用的数学方法,其中组合就是从 n 个元素中抽出 r 个元素(不分顺序��且 (r \leq n)),我们可以简单地将 n 个元素理解为自然数 1, 2, ..., n,从中任取 r 个数。
现要求你输出所有组合。
例如 (n=5, r=3),所有组合为:
123, 124, 125, 134, 135, 145, 234, 235, 245, 345。
输入格式
一行两个自然数 (n, r (1 < n < 21, 0 \leq r \leq n))。
输出格式
注意哦! 输出时,每个数字需要 3 个场宽。以 C++ 为例,你可以使用下列代码:
cout << setw(3) << x;
输出占 3 个场宽的数 x。注意你需要头文件 iomanip。
输入输出样例
| 输入 #1 | 输出 #1 |
|---|---|
| 5 3 | 1 2 3 |
| 1 2 4 | |
| 1 2 5 | |
| 1 3 4 | |
| 1 3 5 | |
| 1 4 5 | |
| 2 3 4 | |
| 2 3 5 | |
| 2 4 5 |
这次的dfs中采用了两个参数,一个表示枚举了几个数,一个表示从哪个数开始往后选,因为这次是组合型枚举,例如,在选了1 3 2之前,1 2 3肯定也已经选过了,所以不会有1 3 2这种情况出现,从哪个数开始往后选,都是选的比这个数字典序大的数,不存在字典数大的数排在字典数小的之前的情况,所以要记录从哪个数开始往后选
#include <bits/stdc++.h>
using namespace std;
int a[25];
int n,r;
void dfs(int x,int start){
//已经选够的情况
if(x > r){
for(int i = 1;i<=r;i++){
cout<<setw(3)<<a[i];
}
cout<<'\n';
return;
}
for(int i = start;i<=n;i++){
a[x] = i;
dfs(x+1,i+1);//选下一个数字,并且下一个数字的字典序要比本次大,也就是从i+1开始往后选
a[x] = 0;
}
}
int main(){
cin>>n>>r;
dfs(1,1);
return 0;
}
扩展练习
***本章节,主要是dfs在枚举方面的应用,未完待续!