图论基础
一、引入:从生活到数学
二、定义图的基本组成
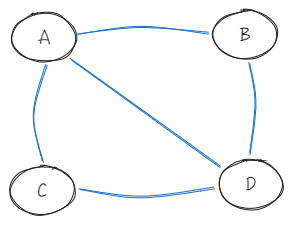
如果我们用数学的语言来描述这个图(抽象),该怎么写呢?
我们可以用 表示一个图,其中 是顶点集(Vertex Set), 是边集(Edge Set)。例如刚才的例子中:
三、互动学习:图的基本术语-度(Degree)
-
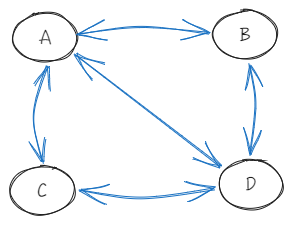
1、这个图中有几个顶点?几条边? “4 个顶点,5 条边。”
-
2、每个顶点连接了几条边?
- 顶点连接的边的数量叫作它的度。例如,顶点 的度是 3,因为 连接了 、 和 。”
计算所有顶点的度
如果你请计算每个顶点的度,并全部加起来的和是多少?
- 10.
- 由此可以发现,图中所有顶点的度加起来等于边数的两倍。
四、路径(path)和环(cycle)
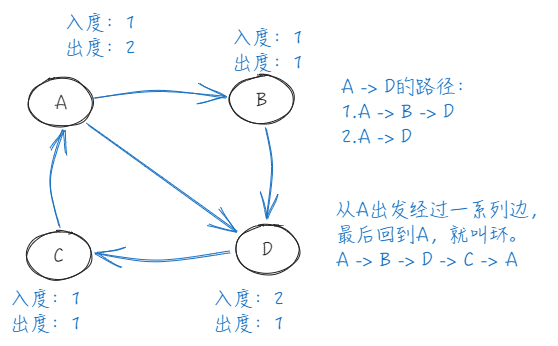
从 走到 ,应该怎么走呢?
- 或 。
- 像这样 从一个顶点到另一个顶点的一系列边,称为路径。
如果从 出发,经过一些边后又回到 ,这就叫做环。
连通性
如果任意两个顶点之间都存在路径,则称这个图是 连通图 。 如果图中有些顶点之间没有路径,则称这个图是 非连通图 。
五、分类
边如果没有方向——无向图
边如果有方向——有向图

边如果有权重——加权图
- 加权图 中每条边都有一个数值,表示某种属性。
- 可以联想每条路有限速
- 加权图 也称 网
网络寻路
国的一个网络使用若干条线路连接若干个节点。节点间的通信是双向的。某重要数据包,为了安全起见,必须恰好被转发两次到达目的地。该包可能在任意一个节点产生,我们需要知道该网络中一共有多少种不同的转发路径。
源地址和目标地址可以相同,但中间节点必须不同。
如图 所示的网络。
是允许的。
或者 都是非法的。
输入数据格式
输入数据的第一行为两个整数 ,分别表示节点个数和连接线路的条数 。
接下去有 行,每行为两个整数 和 ,表示节点 和 联通 。
输入数据保证任意两点最多只有一条边连接,并且没有自己连自己的边,即不存在重边和自环。
输出数据格式
输出一个整数,表示满足要求的路径条数。
输入输出样例
| 输入 #1 | 输出 #1 |
|---|---|
| 3 3 1 2 2 3 1 3 | 6 |
| 输入 #2 | 输出 #2 |
| --- | --- |
| 4 4 1 2 2 3 3 1 1 4 | 10 |
#include<bits/stdc++.h>
#define MAXN 10010
#define MAXM 100010
using namespace std;
int d[MAXN],u[MAXM],v[MAXM];
int main(){
int n,i,m;
long long ans=0;
cin>>n>>m;
for(i=0;i<m;i++){
scanf("%d%d",&u[i],&v[i]);
d[u[i]]++;
d[v[i]]++;
}
for(i=0;i<m;i++){
if(d[u[i]]>1&&d[v[i]]>1)
ans+=(d[u[i]]-1)*(d[v[i]]-1)*2;
}
cout<<ans;
return 0;
}