图的存储方式
邻接矩阵

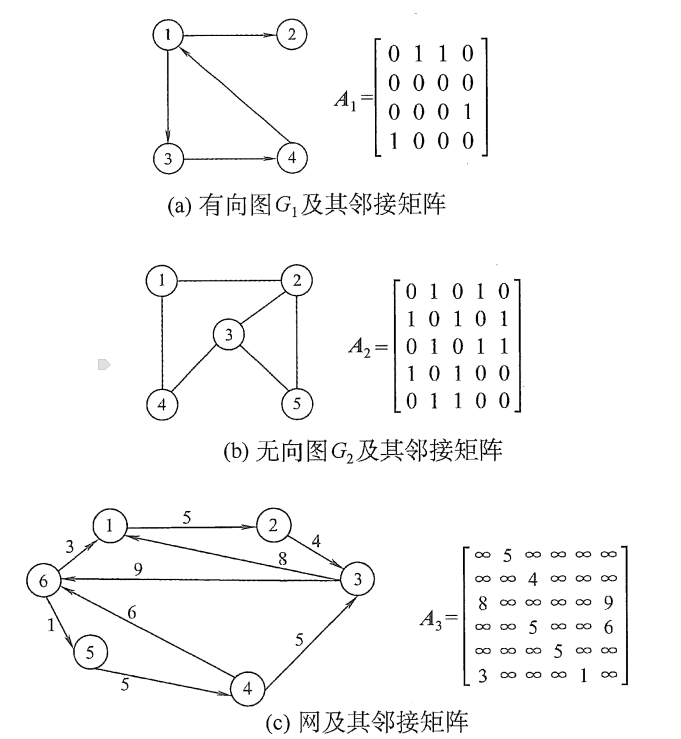

无向图的度
给出N个点,M条边的无向图,不存在重边,给一个节点x,求出该节点的度。 1 < N,M < 1000.
输入格式
第1 行,2 个整数N,M。
接下来M行,每行2个整数Ui,Vi,表示边(Ui,Vi)。
接下来一行一个整数x
输出格式
一个整数。
输入/输出例子1
输入:
4 3
1 2
2 4
4 3
3
输出:
1
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], n, m, x,res;
int main()
{
cin >> n >> m;//输入n个节点和m条边
for (int i = 1; i <= m; i++) {//建立图
int x, y;
cin >> x >> y;
a[x][y]=1; //x到y存在一条边
a[y][x]=1; //y到x存在一条边
}
cin >> x; //输入节点x
for (int i = 1; i <= n; i++) {
if (a[i][x]) {
res++; //结果加1;
}
}
cout << res << endl;
return 0;
}
有向图的出度
给出N个点,M条边的有向图,不存在重边,给一个节点x,求出该节点的出度。
输入格式
第1 行,2 个整数N,M。
接下来M行,每行2个整数Ui,Vi,Wi,表示边(Ui,Vi)的权重为Wi。
接下来一行一个整数x
输出格式
一个整数。
输入/输出例子1
输入:
4 3
1 2 1
2 4 2
4 3 3
3
输出:
0
[1][2][3]填空
#include<iostream>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], n, m, x,res;
int main()
{
cin >> n >> m;//输入n个节点和m条边
for (int i = 1; i <= [1]; i++) {//建立图
int x, y,z;
cin >> x >> y>>z;
[2] ; //x到y存在一条边
}
cin >> x; //输入节点x
for (int i = 1; i <= n; i++) {
if ([3]) {
res++; //结果加1;
}
}
cout << res << endl;
return 0;
}
邻接表

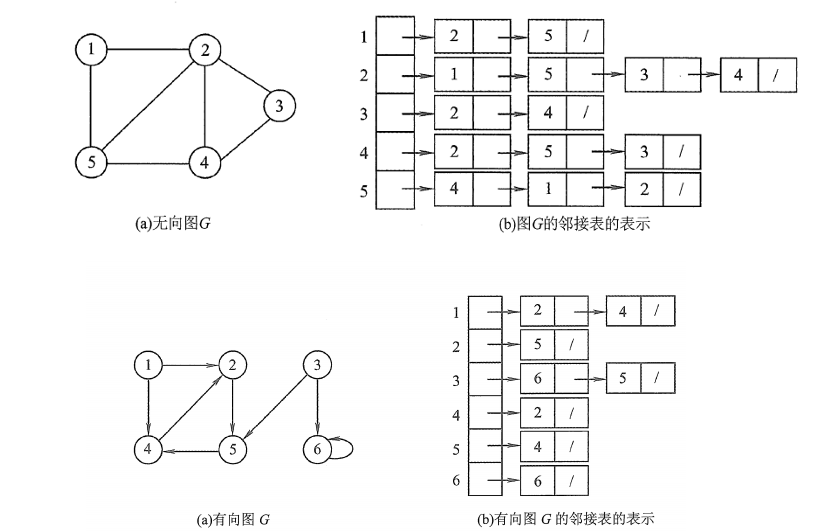

无向图的度
给出N个点,M条边的无向图,可能存在重边但不存在自环,给一个节点x,求出该节点的度。
输入格式
第1 行,2 个整数N,M。
接��下来M行,每行2个整数Ui,Vi,表示边(Ui,Vi)。
接下来一行一个整数x(1 < N,M < 1000000)
输出格式
一个整数。
输入/输出例子1
输入:
4 3
1 2
2 4
4 3
3
输出:
1
静态数组实现邻接表
#include<bits/stdc++.h>
using namespace std;
int N,M;
struct Node {
int v,next;
Node(){ //构造函数1
next=0;
}
Node( int a, int b){ //节点赋值的常见方法
v=a; next=b;
}
};
Node adj[2000002]; //!!!
int idx=1;
int head[1000002];
void insert( int u,int v){
adj[idx] = Node(v, head[u]);//插入一条边
head[u]=idx;
idx++;
}
int main(){
cin >> N >> M;
for (int i=0; i<M; i++) {
int u,v;
cin >> u >> v ;
insert(u,v);
insert(v,u);
}
int x,ans=0;
cin >> x;
for (int i=head[x]; i!=0; i=adj[i].next)
ans++;
cout << ans;
return 0;
}
vector实现邻接表
#include <bits/stdc++.h>
using namespace std;
int main() {
int N, M;
scanf("%d %d", &N, &M);
vector<vector<int>> adj(N + 1); // 邻接表,节点编号从1开始
for (int i = 0; i < M; i++) {
int u, v;
scanf("%d %d", &u, &v);
adj[u].push_back(v);
adj[v].push_back(u);
}
int x;
scanf("%d", &x);
// 节点 x 的度数就是邻接表中 x 的邻居数量
printf("%d\n", (int)adj[x].size());
return 0;
}