二维差分算法
一、 复习一维前缀和与差分
定义:
前缀和数组 b[i] 表示原数组 a[0] 到 a[i] 的和:
b[i] = a[0] + a[1] + ... + a[i]
差分数组 d[i] 表示原数组 a[i] 与 a[i-1] 的差:
b[i] = a[i] - a[i-1]
// 前缀和复习代码
int a[] = {0,1,3,5,7,9}; // 原始数组(1-based)
int b[6] = {0}; // 前缀和数组
for(int i=1; i<=5; i++)
b[i] = b[i-1] + a[i];
// b[3] = 1+3+5=9
int d[6]={0}; //差分数组
for(int i=1; i<=n; i++)
d[i] = a[i] - a[i-1];
2.1 二维前缀和的定义
给定一个二维数组 ( A ),它的前缀和二维数组 ( S ) 中 ( S[i,j] ) 表示以 ( (1,1) ) 为左上角元素,以 ( (i,j) ) 为右�下角元素的矩形块中所有元素的总和。
用公式表示为:
如下图:绿色的部分就表示二位前缀和区块 ( S[3,2] ):
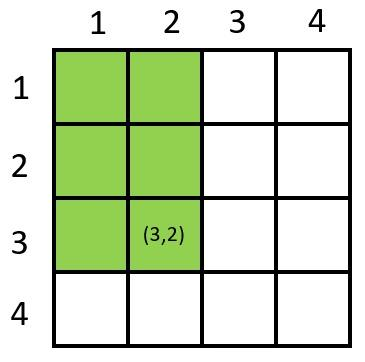
如下图:蓝色的部分就表示差分和区块 ( S[x2,y2] ):
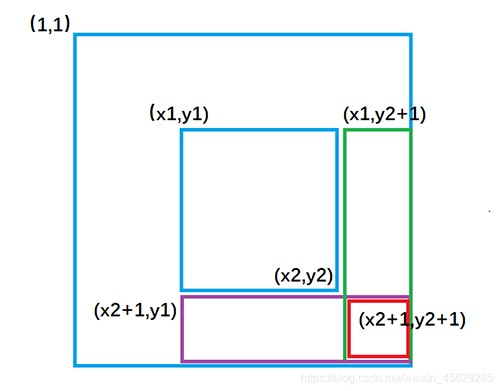
二维差分数组公式表示为:
// 最终通过二维前缀和还原矩阵
for (int i=1; i<=m; i++)
for (int j=1; j<=n; j++)
a[i][j] = a[i-1][j] + a[i][j-1] - a[i-1][j-1] + b[i][j];
算法模板
题目描述:
输入一个 n 行 m 列的整数矩阵,再输入 q 个操作,每个操作包含五个整数 x1,y1,x2,y2,c,其中 (x1,y1) 和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。 每个操作都要将选中的子矩阵中的每个元素的值加上 c。 请你将进行完所有操作后的矩阵输出。
输入格式:
第一行包含整数 n,m,q。 接下来 n 行,每行包含 m 个整数,表示整数矩阵。 接下来 q 行,每行包含 5 个整数 x1,y1,x2,y2,c,表示一个操作。
输出格式:
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵
#include <bits/stdc++.h>
using namespace std;
const int MAX_SIZE = 1e3+0; // 支持的最大矩阵尺寸
int d[MAX_SIZE][MAX_SIZE], a[MAX_SIZE][MAX_SIZE];
int n, m, q;
void insert(int x1, int y1, int x2, int y2, int c)
{
d[x1][y1] += c;
d[x2 + 1][y1] -= c;
d[x1][y2 + 1] -= c;
d[x2 + 1][y2 + 1] += c;
}
void restore() {
// 计算差分矩阵的前缀和,也就是原矩阵的新值
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + d[i][j];
}
int main()
{
scanf("%d%d%d", &n, &m, &q);
// 输入原矩阵,并依次构造差分矩阵
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
scanf("%d", &a[i][j]);
insert(i, j, i, j, a[i][j]);
}
while (q--)
{
int x1, y1, x2, y2, c;
scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
insert(x1, y1, x2, y2, c); // 差分矩阵操作
}
restore();
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
printf("%d ", a[i][j]);
}
printf("\n");
}
return 0;
}