二叉排序树
引入
我们经常需要快速的查找数据,方法有很多,但都有各自的应用场景,比如下图所示的二分查找。
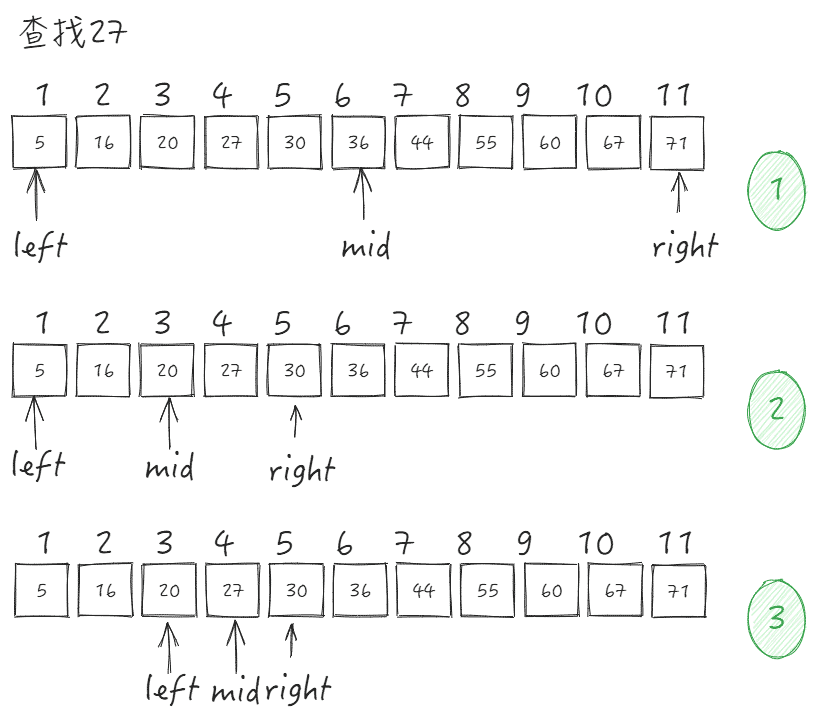
��在上图中可以发现二分查找效率非常高 O(logN)。但是插入或删除一个节点就比较慢了,由于是通过线性表实现的二分查找,插入、删除就会飞铲通过慢。 那么有什么办法可以让插入和删除也尽量快呢? 对了,就是本节的主角——二叉排序树。
二叉排序树的定义
二叉排序树(Binary Search Tree)必须满足以下特点:
- 若左子树不为空,则左子树的所有结点值皆小于根结点值
- 若右子树不为空,则右子树的所有结点值皆大于根结点值
- 左右子树也是二叉排序树
如下图,是一颗二叉排序树:
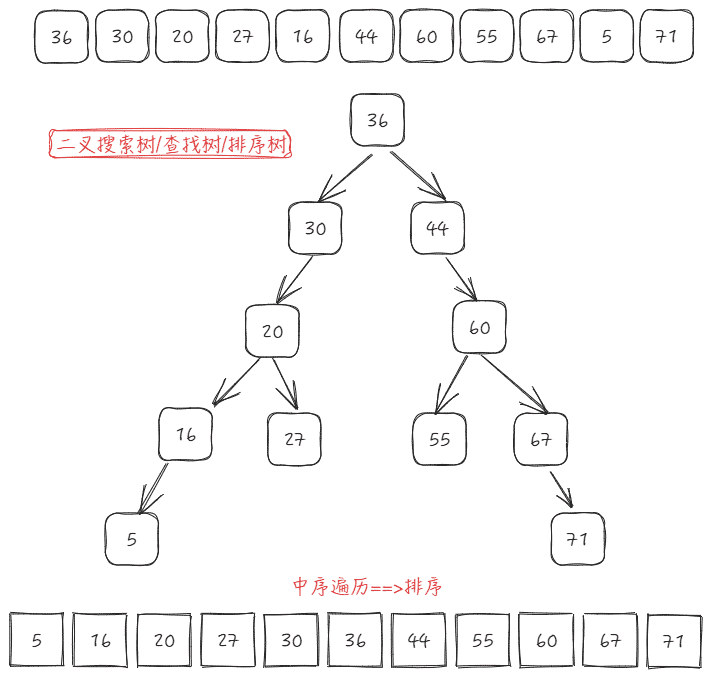
我们对二叉排序树进行中序遍历,可以得到:5,16,20,27,30,36,44,55,60,67,71。刚好是一个从小到大的有序序列,从这一点看,二叉排序树是可以进行排序的,所以这种树又叫二叉排序树(Binary Sort Tree)。
插入
有 N 个随机产生的不同的整数数列,按照输入次序插入到二叉排序树的 C++程序,然后按照中序遍历输出二叉树的节点值。 输入格式 第 1 行:一个正整数 N,不超过 10000。 第 2 行有 N 个不同整数,范围 [-100000,100000]。
输出格式 输出一行 N 个整数,表示相应任务的答案。
输入: 5 2 1 3 -2 6
输出: -2 1 6 3 2
#include<bits/stdc++.h>
using namespace std;
struct BiTNode{
int data; //结点里的值
int lchild, //左孩子的结点指针(数组下标)
rchild; //右孩子的结点指针(数组下标)
} Tree[100005];
int total=1;
int N,root;
void insDFS( int &root, int x) {
if (root==0) { //root 指向的是空树时,申请一个节点给它
Tree[total].data=x;
root = total; //相当于修改了前面传递来的"指针",比如:.lchild
total++;
return ;
}
if (x<Tree[root].data)
insDFS(Tree[root].lchild, x);
else
insDFS(Tree[root].rchild,x );
}
void sDFS( int root){
if (root==0) return ;
sDFS(Tree[root].lchild);
cout << Tree[root].data<<" ";
sDFS(Tree[root].rchild);
}
int main(){
root=0; //空树
cin >> N;
for (int i=0; i<N; i++){
int da;
cin >> da;
insDFS(root,da); //插入 da
}
sDFS(root); //后续遍历
return 0;
}
二叉排序树的查找
有 N 个节点的二叉排序树,编号是 1 到 N。每个节点的信息格式为:(id, data, leftId, rightId),分别为(编号,包含的数值,左子树的编号,右子树的编号)。 现在有 M 个任务,每个任务为:给一个数值,求它是否在树中的某个节点上?如果在,输出对应的节点编号,否则输出-1。
输入格式 第 1 行:一个正整数 N,不超过 100000。 下面 N 行,每行 4 个整数表示一个结点信息数据:lc, data, rc。(id, data, leftId, rightId),分别为(编号,包含的数值,左子树的编号,右子树的编号)。每个结点编号都不相同,从 1 到 N,且每个节点包含的数值(int 型范围)不相同,0 表示空节点,根节点编号为 1。 第 N+1 行一个正整数:M,不超过 100000。 第 N+2 行有 M 个整数(int 型范围),要求其相对应的节点编号,如果找不到就输出-1。 【提示】 数据比较大,建议使用 scanf/printf 读入/输出。 输出格式 输出一行 M 个整数,表示相应任务的答案。
输入:
9
1 8 2 3
2 3 4 5
4 1 0 0
5 6 7 8
7 4 0 0
8 7 0 0
3 10 0 9
9 14 6 0
6 13 0 0
3
6 15 13
输出: 5 -1 6
#include<bits/stdc++.h>
using namespace std;
struct BiTNode{
int id; //编号
int data; //结点里的值
int lchild, //左孩子的结点指针(数组下标)
rchild; //右孩子的结点指针(数组下标)
} Tree[100005];
int N,M;
int search( int root,int x ){
if (root == 0) return -1; //空结点
int y = Tree[root].data;
if ( x == y)
return root;
else if ( x < y )
return search(Tree[root].lchild,x);
else
return search(Tree[root].rchild,x);
}
int main(){
scanf("%d",&N);
for (int i=0; i<N; i++){
int id, lc,da,rc;
scanf("%d%d%d%d",&id,&da,&lc,&rc);
Tree[id].data=da;
Tree[id].lchild=lc;
Tree[id].rchild=rc;
}
cin >> M;
for (int i=0; i<M; i++){
int x;
scanf("%d",&x);
printf("%d ",search(1,x));
}
return 0;
}
二叉排序树和二分查找本质上都是利用了“二分”,很多相似之处,比如以下几方面:
- 都是有序的。二分查找是全部有序,二叉排序数是局部有序。
- 都是将一组数划分成若干区域。二分查找通过三个标志位,二叉排序树通过树结构。
- 都是通过比较目标值和“区域分界点”的大小,从而确定目标值在哪个区域中。在二分查找中与中间标志位比较,在二叉排序树中与根结点比较。
我们在二分查找中说过:当涉及到频繁地插入和删除操作时,二分查找就不合适了。
二叉排序树的删除操作
二叉排序树的查找、插入操作都比较简单易懂,但是它的删除操作就比较复杂了 。针对要删除节点的子节点个数的不同,我们需要分三种情况来处理。 第一种情况是,如果要删除的节点没有子节点,我们只需要直接将父节点中,指向要删除节点的指针置为 null。比如图中的删除节点 55。
第二种情况是,如果要删除的节点只有一个子节点(只有左子节点或者右子节点),我们只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的子节点就可以了。比如图中的删除节点 13。
第三种情况是,如果要删除的节点有两个子节点,这就比较复杂了。我们需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上。然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以,我们可以应用上面两条规则来删除这个最小节点。比如图中的删除节点 18。
(课后作业)