哈夫曼编码

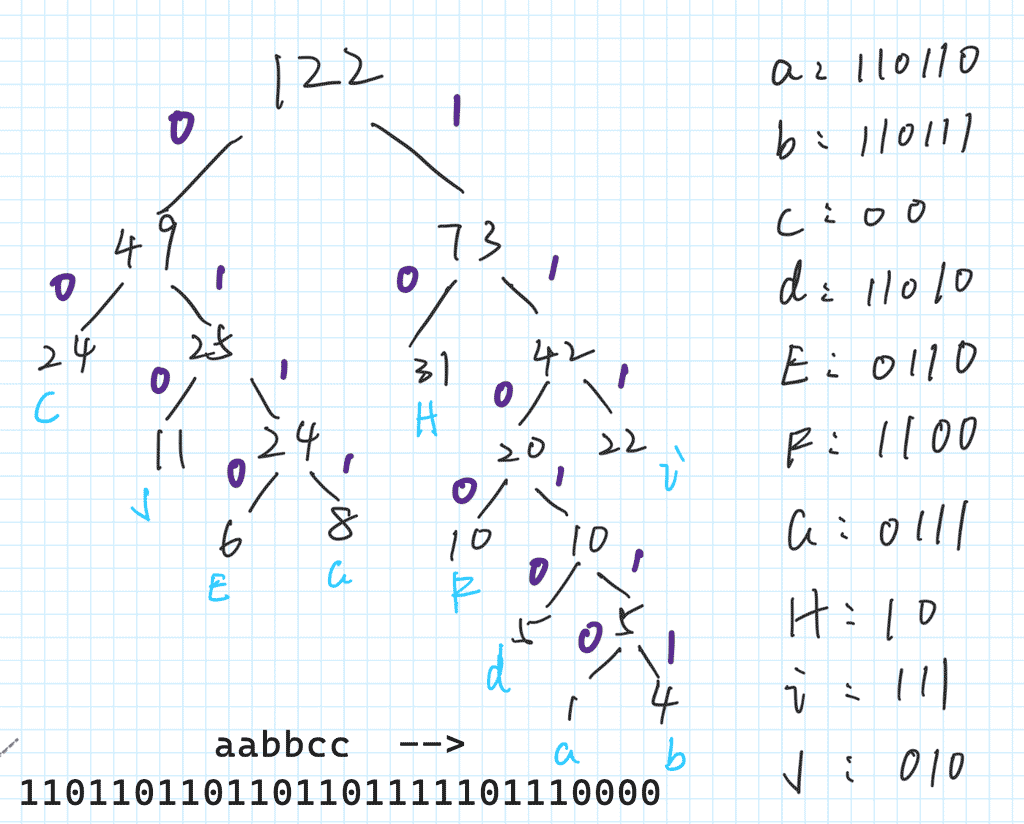
huffman code

构造出哈夫曼树以后，就可以参照上图对原文进行 huffman 编码了！比如：

string plain = "aabbcc";
string huffmancode = encode(plan); 
huffmancode = "1101101101101101111101110000";

!!! 应用堆优化哈夫曼编码的代码修改，点击这里下载！

哈夫曼编码
/*
有有一段要传送的字符串，长度不超过 1M，问怎样设计 Huffman 编码？
输入：
abxxaazbaxax
输出：
a=0
b=101
x=11
z=100
*/
#include <bits/stdc++.h>
using namespace std;
struct Node
{
    int fa, left, right; // 父节点，左右孩子节点
    long long w;         // 权重，出现频次 
    Node()
    { // 初始构造函数
        fa = left = right = w = 0;
    }
    Node(int a, int b, int c, long long d)
    { // 代参数构造函数
        fa = a;
        left = b;
        right = c;
        w = d;
    }
};
Node f[512];     // 存储 huffman 树
int m; //f 数组有效元素个数 

string huf[256]; // 下标是 asccii 码编号，值是对应的编码

string s;     // 读取的原字符串
int sidx = 0; // 读取字符指针
char read();  // 顺序读取一个字符/字节

int charNumber; // 存储字符总数，决定合并次数
void countFrequency();

int findMax1(int);
void findMax2(int, int &, int &);
void createHuffmanTree();
void analysisCode(int root, string code); // Huffman 编码
void printHuffmanCode(); //打印 huffman 编码方案
string encode(); //对原文进行编码
void decode(string buff);

int main()
{
    cin >> s;

    countFrequency();
    
    // 计算编码方案
    createHuffmanTree();

    analysisCode(m, "");
    printHuffmanCode();

    // 对数据编码
    string buff = encode();
    decode(buff);
    
    return 0;
}

void countFrequency()
{
	int slen = s.size();
    for (int i = 0; i < slen; i++)
    {
        f[s[i] - 'a' + 1].w++; // 1-26
    }
    
    charNumber = 0;
    for (int i = 1; i <= 26; i++)
        if (f[i].w > 0)
            charNumber++;
}

void createHuffmanTree()
{
    m = 26;

    for (int i = 1; i < charNumber; i++)
    { // n-1 次合并
        int max1, max2;
        findMax2(m, max1, max2);
        f[++m] = Node(0, max1, max2, f[max1].w + f[max2].w); // 构造函数
        f[max1].fa = f[max2].fa = m;
    }
}

void analysisCode(int root, string code)
{
    if (f[root].left == 0)
    {
        huf[root] = code;
        return;
    }
    analysisCode(f[root].left, code + "0");
    analysisCode(f[root].right, code + "1");
}

void printHuffmanCode() {
	int sumlen=0;
    for (int i = 1; i <= 26; i++)
        if (f[i].w > 0) {
        
            cout << char(i + 'a' - 1) << "=" << huf[i] << endl;
            sumlen += huf[i].size() * f[i].w;
        }
        
    cout<<"sumlen:"<<sumlen<<endl;

}

string encode() {
    int slen=s.size();
    
    string buff="";
    for(int i=0;i<slen;i++) {
        char c = s[i];
        
        buff += huf[c-'a'+1];
    }
    cout<<"encode:("<<buff.size()<<")"<<buff<<endl;
    return buff;
}

void decode(string buff) {
	int curr = m;
	string dbuff="";
	int blen = buff.size();
	for(int i=0;i<blen;i++){
		if(buff[i] == '0')
			curr = f[curr].left;
		else
			curr = f[curr].right;
		if(f[curr].left == 0 && f[curr].right==0){
			dbuff+=curr+'a'-1;
			curr = m;
		}
	}
	cout<<"decode:"<<dbuff<<endl;
}

int findMax1(int m)
{
    long long a = 100000000000LL;
    int ai = 1;
    for (int i = 1; i <= m; i++)
        if (f[i].w > 0 && f[i].fa == 0 && f[i].w < a)
        { // w>0
            a = f[i].w;
            ai = i;
        }
    return ai;
}
void findMax2(int m, int &m1, int &m2)
{
    m1 = findMax1(m);
    f[m1].fa = -1;
    m2 = findMax1(m);
}

备注

Huffman 是最有二叉树，也就是 WPL 最小，那么为什么 WPL 最小，huffman 编码是编码总长最小的方案？

后续练习空间

上面的代码中，对原字符串编码后得到了一长串 10 字符串，比原文还长，是不是不实用？怎么优化？
如果用 huffman 编码将原文件编码后，如果传输给其他人，其他人怎么解码得到原文？
针对给定的原文，最长的一个 huffman 编码怎么求？

*学习笔记

暂没有学习笔记，快来抢first blood ！

哈夫曼编码​

后续练习空间​

*学习笔记​

哈夫曼编码

后续练习空间

*学习笔记