哈夫曼树
一、引言
1、信号传输的速度的思考 光的速度是多少? 非常快,一刹。 电子在电路里的传输速度,理论上也是接近光速的。但是既然是这样,为什么我们传输数据的速度为什么不是光速?2004 年以前,我们用 ADSL,速率 512kbps(更慢的拨号�上网 56K),2004 年以后,我们用光纤,速率 100Mbps,但是,我们传输数据的速度为什么还是达不到光速?
要想完全了解这个问题,需要了解信号传输的物理原理和一系列的编码调制算法。内容非常多,可以写几车的书了。

在此,我通俗的比喻一下(如上图): 网线/光纤/wifi 就像一条高速公路,我们要传输的信息/数字(0、1)就像一辆辆汽车载的货物,车速就是信号的传输速度,载货量就是数据量。 如果这条高速公路的速度上限是光速,但是汽车的速度却还达不到光速,也就数据传输速率达不到光速。
车速收到很多因素影响(引擎、路况、天气),载货量也受到很多因素的影响(车速、车厢大小、物品摆放方法)。
为了更快,我们不断提高车速,包括硬件层面(更快的引擎——更快的设备/线路),和软件层面(更轻容量更大的车厢、物品摆放方法——更优的信息调制算法)。实现上非常复杂,但是宏观原理上就是这么简单。
硬件层面,在此不谈,我们讨论下软件层面,也就是怎么让同样的车速,装载更多的货物。
2、数据压缩的思考 在同样的车速下,如何装载更多的货物? 同理,在信息传输中,如何用更少的 0、1 表示更多的信息?这就是信息学的一个重要研究领域,每一个突破让网速提高一个大的台阶,给信息化带来巨大的进步。
关于更少的 0、1 表示更多的信息,最直接想到的一个方法就是——压缩。
如果你的电话号码是 138 6666 6666,你会告诉别人:一三八 8 个六? 你要参加 Certified Software Professional Junior,我们会说 CSP-J? 更常见的文言文相对于白话文是不是也是压缩?
所以数据压缩是信息技术中非常重要的一个领域,因为它对于硬件几乎没有要求,只要软件层面进行优化。
数据压缩算法也可以写几车书,今天我们正题是:最著名的、影响最深远的算法之一,叫做哈夫曼编码。
3、哈夫曼树的诞生 1951 年,哈夫曼在麻省理工学院(MIT)攻读博士学位,他和修读信息论课程的同学得选择是完成学期报告还是期末考试。导师罗伯特·法诺(Robert Fano)出的学期报告题目是:查找最有效的二进制编码。由于无法证明哪个已有编码是最有效的,哈夫曼放弃对已有编码的研究,转向新的探索,最终发现了基于有序频率二叉树编码的想法,并很快证明了这个方法是最有效的。哈夫曼使用自底向上的方法构建二叉树,避免了次优算法香农-范诺编码(Shannon–Fano coding)的最大弊端──自顶向下构建树。 1952 年,于论文《一种构建极小多余编码的方法》(A Method for the Construction of Minimum-Redundancy Codes)中发表了这个编码方法。
二、哈夫曼树基础
路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。
通路中分支的数目称为路径长度。若规定根结点的层数为 1,则从根结点到第 L 层结点的路径长��度为 L-1。
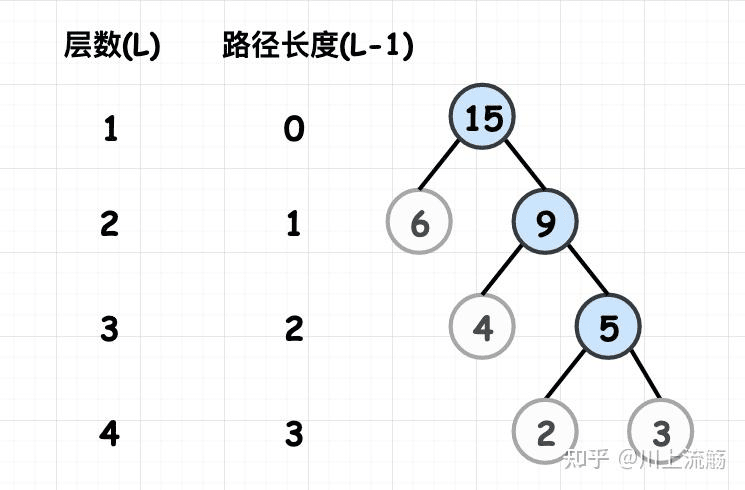
节点的权和带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
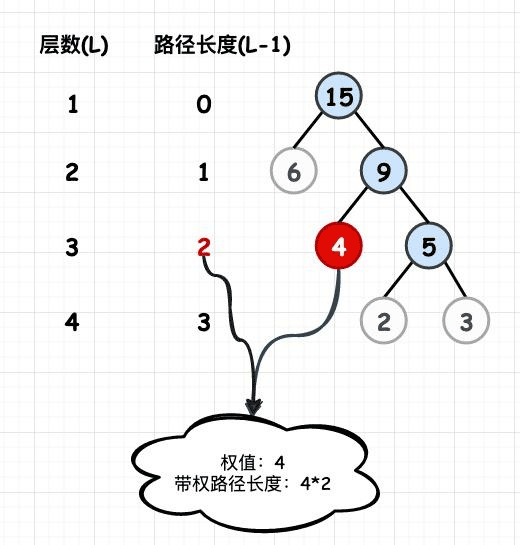
树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为 WPL。
如上图:数的带权路径长度为:
WPL = (2+3) * 3 + 4 * 2 + 6 * 1 = 29
三、哈夫曼树的构造
哈夫曼树(Huffman Tree),又称霍夫曼树,是一种特殊的带权路径长度最短的二叉树。它是由美国计算机科学家大卫·哈夫曼(David A. Huffman)在 1952 年提出的。哈夫曼树主要用于数据压缩领域,特别是用于无损数据压缩的哈夫曼编码。
假设有 n 个权值,则构造出��的哈夫曼树有 n 个叶子结点。 n 个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
(1) 将 w1、w2、…,wn 看成是有 n 棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3) 从森林中删除选取的两棵树,并将新树加入森林;
(4) 重复 (2)、(3) 步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
例如:对 2,3,4,6 这四个数进行构造
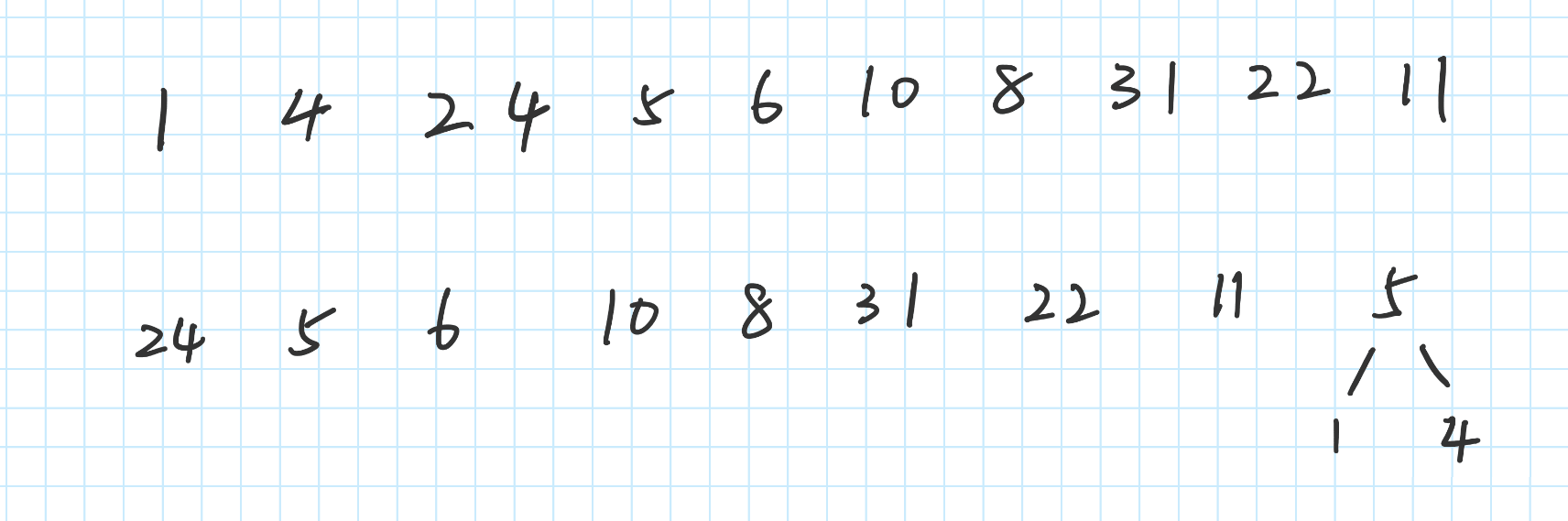
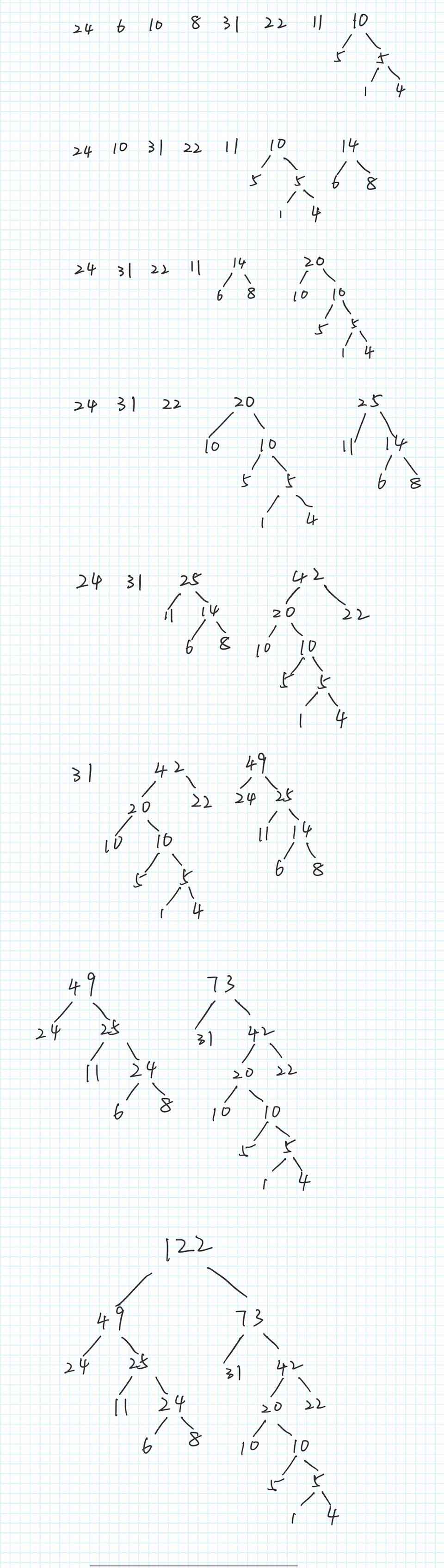
/*
有有一段要传送的字符串,长度不超过 1M,问怎样设计 Huffman 编码?
输入:
abxxaazbaxax
输出:
a=0
b=101
x=11
z=100
*/
#include<bits/stdc++.h>
using namespace std;
struct Node{
int fa,left,right; //父节点,左右孩子节点
long long w; //权重
Node(){ //初始构造函数
fa=left=right=w=0;
}
Node(int a, int b, int c, long long d){ //代参数构造函数
fa=a; left=b; right=c;w=d;
}
};
int n,m;
Node f[100]; //会调用初始构造函数
string huf[27]; // 编码
int findMax1( int );
void findMax2( int, int & , int &);
void DFS( int root, string code); //Huffman 编码
int main(){
string s;
cin >> s;
for (int i=0; i<s.size(); i++){
f[ s[i]-'a'+1].w++; //1-26
}
n=0;
for (int i=1; i<=26; i++)
if (f[i].w>0)
n++;
m=26;
for (int i=1; i<n; i++){ //n-1 次合并
int max1,max2;
findMax2(m,max1,max2);
f[++m] =Node(0, max1, max2, f[max1].w+f[max2].w);//构造函数
f[max1].fa=f[max2].fa=m;
}
DFS( findMax1(m),"");
for (int i=1; i<=26; i++)
if (f[i].w>0)
cout <<char(i+'a'-1)<<"="<< huf[i]<<endl;
return 0;
}
int findMax1( int m){
long long a=100000000000LL;
int ai=1;
for (int i=1; i<=m; i++)
if (f[i].w>0 && f[i].fa==0 && f[i].w<a){ // w>0
a=f[i].w;
ai = i;
}
return ai;
}
void findMax2( int m, int &m1 , int &m2){
m1 = findMax1(m);
f[m1].fa=-1;
m2 = findMax1(m);
}
void DFS( int root, string code){
if ( f[root].left==0){
huf[root]=code;
return;
}
DFS(f[root].left,code+"0");
DFS(f[root].right,code+"1");
}
四、总结哈夫曼树的特点
1. 带权路径长度最短:
- 哈夫曼树是一种优化的二叉树,其中每个叶节点都有一个权重(通常对应于字符的频率),树的带权路径长度(即所有叶节点的权重与其路径长度的乘积之和)被最小化。
2. 贪心算法构建:
- 哈夫曼树的构建过程是一个贪心算法的过程。它从一组权重开始,逐步构建树,直到只剩下一个节点(树的根节点)。
3. 叶节点:
- 哈夫曼树的叶节点代表输入数据中的符号(如字符),每个叶节点都有一个与之关联的权重。
4. 内部节点:
- 哈夫曼树的内部节点不代表实际的符号,它们只是用于构建树的结构,其权重是其子节点权重的总和。
5. 路径和编码:
- 从哈夫曼树的根节点到每个叶节点的路径定义了相应符号的哈夫曼编码。通常,路径上的左分支代表 0,右分支代表 1。
6. 最优性:
- 哈夫曼树是最优的前缀码,意味着任何一种编码方案都不会有比哈夫曼编码更短的平均码长。
7. 应用:
- 哈夫曼树广泛应用于数据压缩领域,如文件压缩、图像压缩、音频压缩等。