树的定义
引入
在现实中,不论是人类社会还是大自然,都有这样一类关系,即层次关系。
比如,大树与树枝、叶子, 家族中的祖孙三代,组织中的领导和下属,操作系统中的文件和文件夹,数据库中的表和表字段,编程语言中的变量和函数,��等等。
这类关系一般还包含一对多的关系,即一个对象可以有多个子对象。

一对多的层次关系跟大树与枝叶的关系非常相似,于是在计算机科学中,为了表示/抽象这类关系,就定义了树的结构。
一、什么是树
树是计算机科学中非常常见的一种数据结构。它们按节点层次结构进行组织。存储在树中的任何内容都用一个节点表示,该节点可以包含自己的数据以及对其子项(子节点)的引用。 树的定义有如下两个限定条件:
- 树的所有节点都必须通过父子关系的路径以某种方式连接。
- 树中的两个节点之间可以有且只能有一条路径。
由以上两个条件,我们可以得出�树的两个特性:
- 树中只能有一个根节点。
- 树中不能有任何循环,即子孙节点不相交
- 子节点本身就是一棵树。
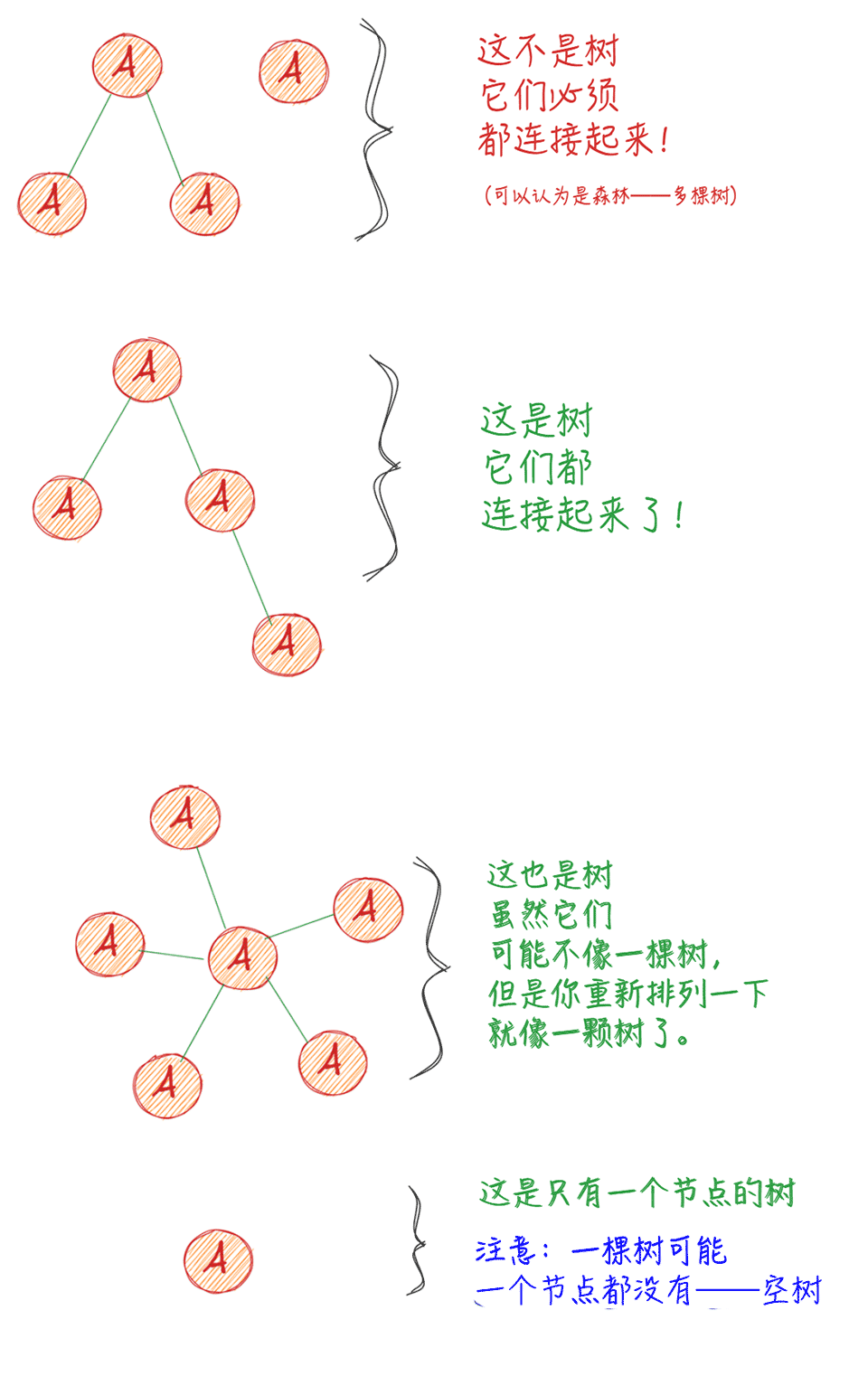
上图中的 A 是一个包含元素的集合,通常称为节点(node)。它可以存储任何数据项,无论是名称、地点、数字等,还是任何类型的。
树(Tree)是由 N (N >= 0) 个结点构成的有限集合。
当 N = 0 时,树为空树 当 N = 1 时,树只有一个根结点 当 N > 1 时,树除了一个根结点外,其余结点又可分为若干个不相交的有限集合,我们称之为子树。
非空树有且仅有一个根结点。
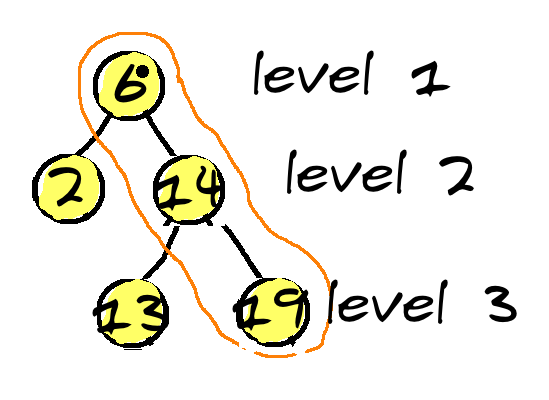
树的层级
很自然的我们就想到了树是一层一层的,就像一个祖父是根,父母、姑、舅、姨是一辈,你、兄、弟、姐、妹是第三辈,所以树也有层级,即定义了树的深度。
二、树相关的术语
树的结构我们清楚了,但是为了沟通交流方便,科学家们定义了很多相关的术语,我们按图索骥,来认识树的相关名词。
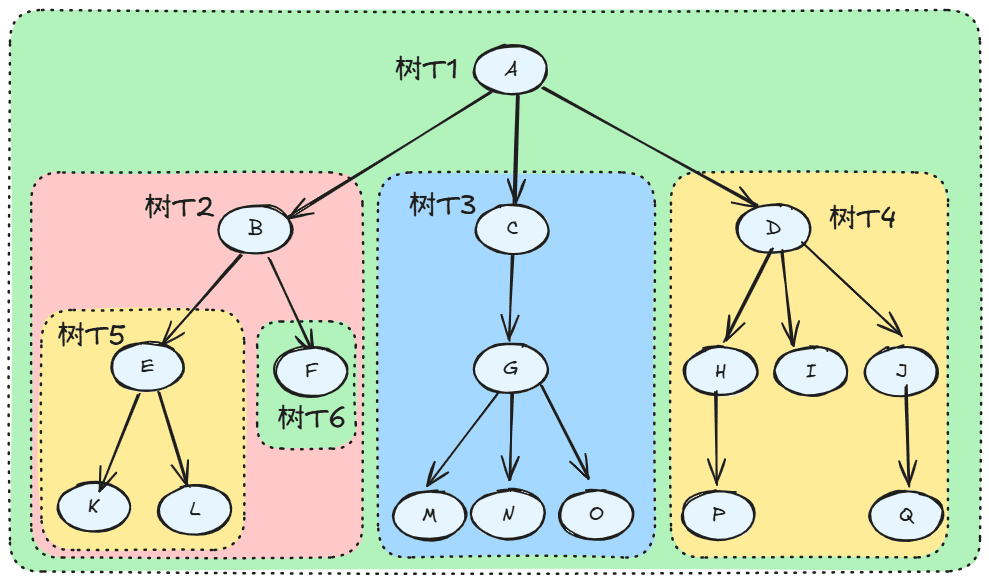
子树:树是一个有限集合,子树则是该集合的子集。就像套娃一样,一棵树下面还包含着其子树。 比如,树 T1 的子树为 树 T2、T3、T4,树 T2 的子树为 T5、T6. 上图中还有许多子树没有标记出来。
节点(Node):一个节点包括一个数据元素和若干指向其子树分支。 比如,在树 T1 中,节点 A 包括一个数据元素 A 和 三个指向其子树的分支。上图中共有 17 个节点。
根节点(Root):一颗树只有一个树根,这是常识。在数据结构中,“树根”即根节点。 比如,节点 A 是树 T1 的根节点;节点 C 是树 T1 的子节点,是树 T3 的根节点。
度(Degree):一个节点拥有的子树数。 比如,节点 A 的度为 3,节点 G 的度为 3,节点 H 的度为 1.
叶子(Leaf)/ 终端节点:度为 0 的节点被称为叶子节点,很形象吧。 比如,对于树 T1 来说,节点 F、I、K、L、M、N、O、P、Q 均为叶子。
分支节点 / 非终端节点:和叶子节点相对,即度不为 0 的节点。
内部节点:顾名思义,在树内部的节点,即不是根节点和叶子节点的节点。
孩子(Child)、双亲(Parent)、兄弟(Sibling)、堂兄弟、祖先、子孙这些概念和族谱上的相同。 比如,对于节点 B 来说:节点 A 是其双亲节点,节点 E、F 是其孩子节点,节点 C、D 是其兄弟节点,节点 K 是其子孙节点。
层次(Level):从根节点开始,根为第一次,根的孩子为第二层,依次往下。 比如,节点 K 在树 T1 中的层次为 4.
深度(Depth)/ 高度:指树的最大层次。 比如,树 T1 的深度为 4.
有序树:如果节点的各子树从左到右是有次序的、不能颠倒,则为有序树,否则为无序树。对于有序树的孩子来说,最左边的孩子称为第一个孩子,最右边的孩子称为最后一个孩子。 比如,如果树 T1 是一个有序树,则其根节点的第一个孩子为节点 B,最后一个孩子为节点 D.
三、树和线性表的比较
比较
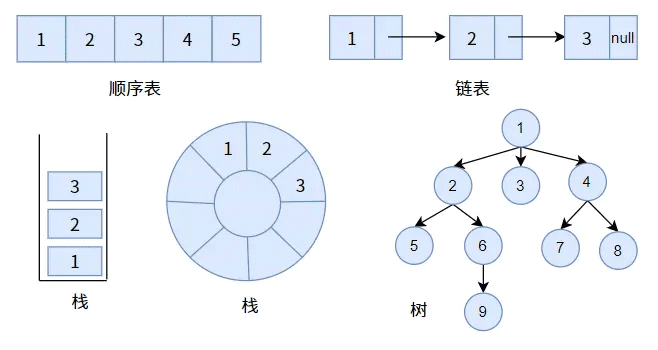
看图直观体验何为(前驱结点和后继结点间)一对一的关系,何为(双亲结点和孩子结点之间)一对多的关系。
四、总结
- 一对多的层次关系,非线性表。
- 树的所有节点都必须通过父子关系的路径以某种方式连接。
- 树中的两个节点之间可以有且只能有一条路径。
- 树中只能有一个根节点。
- 树中不能有任何循环,即子孙节点不相交。
- 子节点本身就是一棵树,所以树的定义是递归的。
五、思考
树的节点的孩子数量是没有限制的,即,你想要几个孩子就要几个孩子,想分几个叉就分几个叉。 如果是两个叉,就是 二叉树 吗?