跳到主要内容

堆

引入​

“二叉”自不必多说，本章主要介绍的树都是二叉树。那么啥是“堆”呢？ 我们在日常生活中，通常会说“一堆东西”或者“堆东西”，这里的“堆”，通常指重叠放置的许多东西。

一堆木头

我们在堆东西的时候，肯定都有一个经验，即：为了使这堆东西更稳定，会将比较重的、大的东西放在下面，比较轻的、小的东西放在上面。 这个经验放在数据结构——二叉树中，同样适用。只不过“重”“大”是根据结点值的大小来判断的，而且扩展一下最顶端的值可以是最小或最大。

堆（heap）的定义​

堆（heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：

l 堆中某个结点的值总是不大于或不小于其父结点的值；

l 堆总是一棵完全二叉树。

小根堆

它是一颗完全二叉树。事实上，该二叉堆就是由完全二叉树经过调整转化而来； 任何一个双亲结点的值，均小于或等于左孩子和右孩子的值； 每条分支从根结点开始都是升序排序（如分支 1-2-3-4）。

这样的二叉堆被称为小根堆，它的堆顶，即根结点 A，是整棵树的最小值。

大根堆

与小根堆相对应的是大根堆：

大根堆是一颗完全二叉树； 它的任何一个双亲结点的值，均大于或等于左孩子和右孩子的值； 每条分支从根结点开始都是降序排序。 大根堆的堆顶，是整棵树的最大值。

堆的存储​

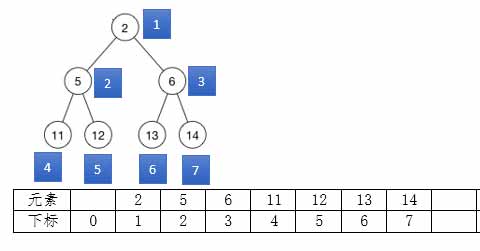
静态数组存储堆

堆的数据结构逻辑上是二叉树，但存放在一维数组里：
堆的根下标为 1；
堆第 i 个元素的左孩子是第 2i 个元素；
堆第 i 个元素的右孩子是第 2i+1 个元素；

向上调整（up，上升，插入）​

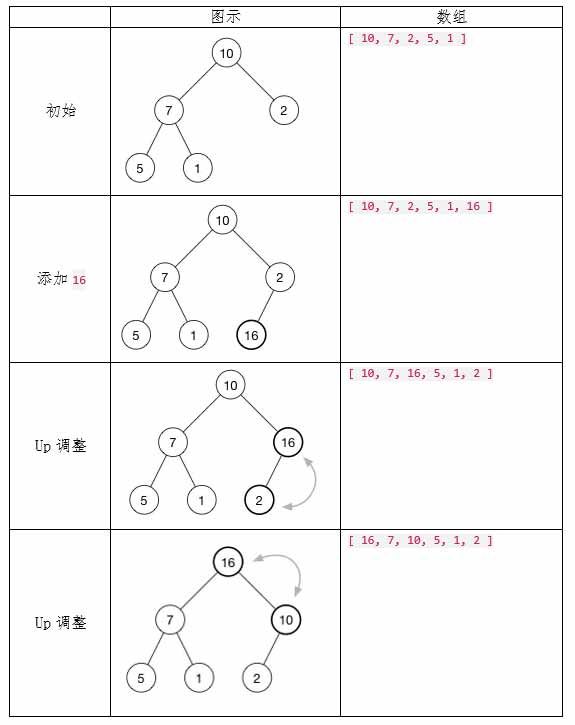
堆插入-向上调整

//读入 n 个整数，使用向上调整算法 UP()，建立大根堆。然后输出堆数组。
using namespace std;
int n;
int f[2002]; 

void up(int i){
    while(i>1 && f[i/2]<f[i]) {
        swap(f[i/2],f[i]);
        i = i/2;
    }
}

int main(){
    cin >> n;
    for (int i=1; i<=n; i++){
       cin >> f[i];
       up(i);
    }
    for (int i=1; i<=n; i++)
      cout << f[i]<<" ";
    return 0;
}

向下调整（down，下沉，取堆顶）​

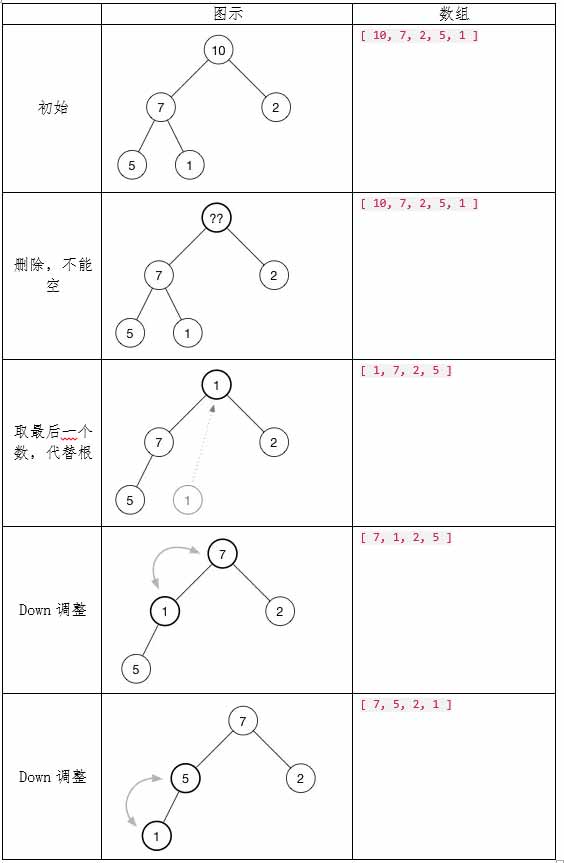
堆取堆顶-向下调整

// 读入 n 个整数后，使用向下调整算法 Down()，建立小根堆。 先输出堆数组， 然后排序输出。
#include<bits/stdc++.h>
using namespace std;
int n;
int f[2002];

void down(int i){
    while (i+i<=n){
      int j=i+i;
      if (j<n && f[j]>f[j+1])
        j++;
      if (f[j]>=f[i])
        break;
      	swap(f[j],f[i]);
      i=j;
    }
}
int main(){
    cin >> n;
    for (int i=1; i<=n; i++)
        cin >> f[i];
    for (int i=n/2; i>0; i--) //初始建堆
        down(i);   
    for (int i=1; i<=n; i++)
      cout << f[i]<<" ";
   cout << endl;
    hsort(); //排序输出
    return 0;
}

应用​

sort: 排序​

//接上面的代码
void hsort( ){   
    while (n>0){
        cout << f[1]<<" ";
        swap(f[1],f[n]);
        n--;
        down(1);
    }
}

优先队列（取最小值）​

？ 你能想到那些应用场景？ 哈夫曼编码中代码修改

总结​

1. 知识点总结​

  • 堆的定义：堆是一个完全二叉树，可以分为大根堆和小根堆。大根堆的堆顶是最大值，小根堆的堆顶是最小值。
  • 存储方式：堆通常使用一维数组来存储，节点按照从上到下、从左到右的顺序依次存入数组中。
  • 节点关系：对于节点 i：
    • 父节点的下标为 i / 2
    • 左子节点的下标为 i * 2
    • 右子节点的下标为 i * 2 + 1
  • 大根堆：堆顶元素是整个堆中的最大值。

2. 学习难点分析​

  • 理解完全二叉树的概念：完全二叉树的特性是每个节点要么有 0 个或 2 个子节点，并且最后一层的节点尽可能靠左。理解这一点对于掌握堆的存储方式至关重要。
  • 节点下标的计算：需要熟练掌握如何通过节点的下标计算其父节点和子节点的下标。这在实现堆的操作时非常重要。
  • 堆的性质：理解大根堆和小根堆的性质，特别是堆顶元素的特性，这对于设计和实现堆排序等算法非常关键。

3. 学习建议​

  • 多画图：通过手绘二叉树来帮助理解和记忆堆的结构。可以在纸上画出不同的堆结构，标注每个节点的下标及其父节点和子节点的关系。
  • 动手实践：编写代码实现堆的基本操作，如插入、删除、调整等。通过实际编程来加深对堆的理解。
  • 理论与实践结合：先学习理论知识，再通过具体的编程练习来巩固。可以尝试解决一些与堆相关的算法题，如堆排序、优先队列等。
  • 多角度思考：不仅要理解堆的数据结构，还要思考为什么这样设计，它的优势在哪里，以及它在实际应用中的场景。

难题挑战​

*学习笔记​

暂没有学习笔记，快来抢first blood ！