跳到主要内容

二叉树基础

一、二叉树的定义​

二叉树是每个节点最多有两个孩子节点（即每个节点的度最大为 2）的有序树。 定义为左子树和右子树，左子树和右子树是有顺序的，不能颠倒。

  • 二叉树：每个节点最多有两个孩子节点。
  • 有序树：左子树和右子树是有顺序的，不能颠倒。
  • 重要术语：节点、根节点、叶子节点、父/母节点、子节点、子树、层次、深度、路径等。

二、二叉树的类型​

  1. 空二叉树：没有任何节点。
  2. 单节点二叉树：只有一个根节点。
  3. 多节点二叉树：有多个节点。
  4. 左子树为空的二叉树
  5. 右子树为空的二叉树
  6. 满二叉树：每一层的节点数都达到最大值，即一个深度为 d 的满二叉树有 2^d - 1 个节点。
  7. 完全二叉树：除了最底层外，每层节点都充满，且最底层从左向右连续填充
  8. 平衡二叉树：任意节点的左右子树的高度差不超过 1。

满二叉树与完全二叉树 的 区分 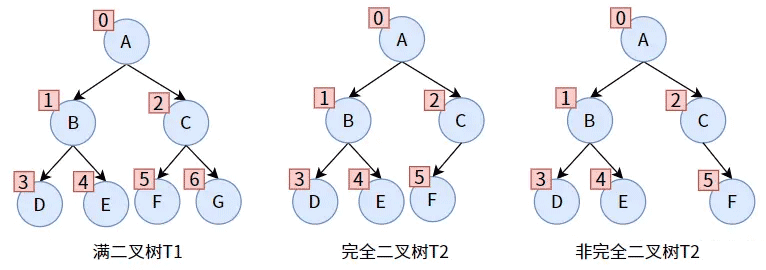满二叉树与完全二叉树 二叉树是有序树，对一颗满二叉树和一颗完全二叉树按「自上向下，自左向右」的顺序进行编号，如上图。

完全二叉树中的所有结点的编号必须和满二叉树的相同编号的结点在位置上完全相同。

换句话说，完全二叉树的结点按「自上向下，自左向右」的顺序不能中断。T3 的结点 C 没有左孩子，显然按那个顺序是中断的。

备注

二叉树是由根结点、左子树、右子树这三部分递归地组合而成的。

三、二叉树的存储​

  1. 顺序存储：使用线性表存储二叉树，适合完全二叉树。
  2. 链式存储：使用链表存储二叉树，适合任意二叉树。
  3. 静态链表：使用数组模拟链表，适合任意二叉树。
  4. 动态链表：使用链表存储二叉树，适合任意二叉树。
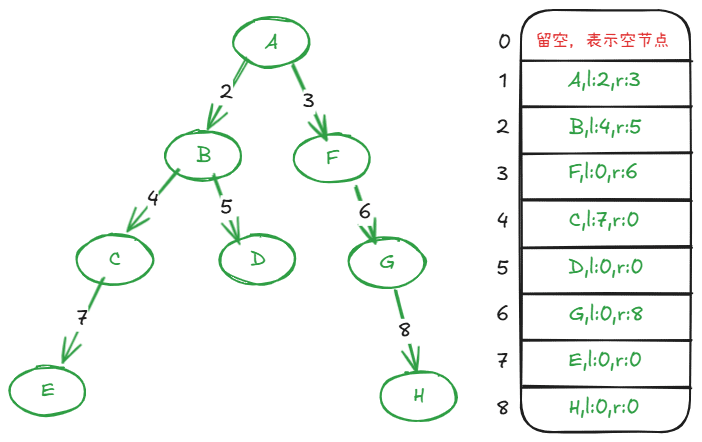
  5. 静态数组：使用数组存储二叉树，适合完全二叉树。 静态数组，根节点一般存储在数组下标为 1 的位置。

静态数组存储二叉树

struct BTNode{
  int data;      //结点里的数
  int lchild,    //左孩子的结点指针（数组下标）
  int rchild;       //右孩子的结点指针（数组下标）
} btnode[1000];
构建树
/* 输入数据：
A 2 3
B 4 5
F 0 6
C 7 0
D 0 0
G 0 8
E 0 0
H 0 0 
*/

int n ;
cin>>n;
for(int i=1; i<=n; i++){
  cin>>btnode[i].data>>btnode[i].lchild>>btnode[i].rchild;
}

求二叉树的深度​

求二叉树的深度
int max_depth = 0;
int get_depth(int root){
  if(root == 0) return 0;
  BTNode node = btnode[root];   
  if(node.lchild == 0 && node.rchild == 0) return 1;
  if(node.lchild != 0)
    max_depth = max(max_depth, get_depth(node.lchild));
  if(node.rchild != 0)
    max_depth = max(max_depth, get_depth(node.rchild));
  return max_depth + 1;
}
//...
cout<<get_depth(1);

常见操作：

  • 查找元素：在二叉树中查找给定值的节点。
  • 插入元素：在二叉搜索树中插入一个新节点。
  • 删除元素：在二叉搜索树中删除一个节点（涉及到左子树最大值或右子树最小值的替换，比如队、平衡树等）。

四、二叉树的遍历​

教学生了解如何遍历二叉树，并用不同的遍历方式来解决问题。可以使用图示和代码示例来说明。

  1. 前序遍历/先序遍历（Pre-order Traversal）：
  • 访问根节点
  • 遍历左子树
  • 遍历右子树
前序遍历/先序遍历
void pre_order_traversal(int root) {
    if (root == 0) return;
    cout << btnode[root].data << " ";
    pre_order_traversal(btnode[root].lchild);
    pre_order_traversal(btnode[root].rchild);
}
//接上面的数据，输出结果为：A B C E D F G H
备注

何时使用？您可以使用 pre-order 遍历来创建树的副本，因为您可以在其子树之前访问每个节点。它还用于获取表达式树上的表达式。 注意：该算法相当于著名的图算法深度优先搜索 （DFS）。

  1. 中序遍历（In-order Traversal）：
  • 遍历左子树
  • 访问根节点
  • 遍历右子树
中序遍历
void in_order_traversal(int root) {
    if (root == 0) return;
    in_order_traversal(btnode[root].lchild);
    cout << btnode[root].data << " ";
    in_order_traversal(btnode[root].rchild);
}
//接上面的数据，输出结果为：E C B D A F G H
备注

何时使用？使用 BST 时，按顺序遍历将按升序给出元素，这对于顺序很重要的问题很有用。

  1. 后序遍历（Post-order Traversal）：
  • 遍历左子树
  • 遍历右子树
  • 访问根节点
后序遍历
void post_order_traversal(int root) {
    if (root == 0) return;
    post_order_traversal(btnode[root].lchild);
    post_order_traversal(btnode[root].rchild);
    cout << btnode[root].data << " ";
}
//接上面的数据，输出结果为：E C D B H G F A
备注

何时使用？您可以使用后序遍历来删除树，因为您可以在删除节点的所有子节点之后再删除根节点。

  1. 层次遍历（Level-order Traversal）：
  • 使用队列，逐层遍历节点
层次遍历
int head=0,tail=0;
BTNode t[100],*q[1000];
void level_order_traversal(int root) {
    if (root == 0) return;
    q[tail++]=btnode[root];
    while (head!=tail) {
        BTNode *node=q[head++];
        cout << node->data << " ";
        if (node->lchild) 
          q[tail++]=node->lchild;
        if (node->rchild) 
          q[tail++]=node->rchild;
    }
}
//接上面的数据，输出结果为：A B F C D G E H
备注

何时使用？您可以使用层次遍历来查找树的宽度，因为您可以逐层遍历节点。类似于广度优先搜索（BFS）。

五、总结​

  1. 二叉树每个节点最多有左右两个子节点，左右有序。
  2. 二叉树的类型很多，特别注意区分满二叉树和完全二叉树。
  3. 二叉树的存储方式有顺序存储和链式存储两种，特别注意静态链表和动态链表的实现。本节重点讲解了顺序存储的静态数组实现。
  4. 二叉树的遍历方式有前序遍历、中序遍历、后序遍历和层次遍历四种。

六、二叉树的高级应用​

  1. 哈夫曼树：用于数据压缩算法。
  2. 二叉搜索树（BST）：每个节点的左子树所有值小于自身，右子树所有值大于自身。
  3. 自平衡二叉查找树（如 AVL 树，红黑树）：
  • AVL 树：任意节点的左右子树高度差最多为 1。
  • 红黑树：具有颜色属性的二叉搜索树，确保树的平衡性。
  1. 线索二叉树：在通常的二叉树节点中，加入前驱和后继的信息。

七、课后练习题​

1、二叉树的遍历​

在线练习：B3642 二叉树的遍历 去练习 在线 OJ

2、二叉树的深度​

在线练习：P4913 二叉树的深度 去练习 在线 OJ

3、根据后序和中序遍历结果重构二叉树​

已知二叉树的后序遍历结果为：E C D B H G F A， 中序遍历结果为：E C B D A F G H， 现在要求重新构造出二叉树，并就后序遍历输出结果。

练习题目： P1827 美国血统 American Heritage 去练习 在线 OJ

*学习笔记​

暂没有学习笔记，快来抢first blood ！